A-star algorithm
Authors: Andrés E. Blanco, Ariel Barboza, Grace Soto, Idan Mika, Lauren Moore [SYSEN 5800, Fall 2021]
Introduction
Algorithms have many purposes in the world of optimization, from Gradient Descent to Belman-Ford, algorithms have been used widely in the world of optimization. Hoping to create better pathing for their new robot, the Shakey project of DARPA created the A-star (A*) a shortest path algorithm that uses heuristics to navigate a terrain. Since then, A* has many modern applications in computer science one of which is the optimal travel path between two locations based on travel time or distance. Optimal path traveled is increasingly important throughout society.
Today more than ever Americans see the importance of the transportation infrastructure. Whether it is the supply chain pipeline or personal travel, transportation is a key part of everyday life. This is extenuated by the climate impacts of travel with the National Geographic society stating “Globally, transportation accounts for between 15 and 20 percent of emissions each year. Motor vehicles are the leading cause of air pollution in the United States, though other modes of travel, such as planes and cruise ships, create greater emissions per voyage per person.” (National Geographic Society) Air pollution, time spent traveling, cost of transportation and the safety associated with transportation impacts individuals every day. Reliable and fast transportation is especially important in the United States where access to transportation can be a barrier to economic and social success.
A* Algorithm can optimize this travel through finding the shortest, cheapest, and most efficient path between two points helping to lower the travel time of everyday travelers, more efficiently conduct cross country shipments and lower the emission production of cars as they travel. By creating a heuristic for and minimizing the travel distance, time and fuel usage while still resulting in a completed trip. This document will introduce the situation of an optimized trip from Cornell University to Harvard University using the A* Algorithm impacted by the travel distance, time and fuel usage parameters.
Theory, Methodology, and Algorithmic Discussions
From its start as a path finding algorithm for a robot, A* Algorithm has grown to be a staple in modern optimization of shortest path algorithms. A* was built originally as a greed algorithm finding an initial solution and improving upon it while remaining in the created bounded space. According to "Integer programming" by Laurence Wolsey "The idea of a greedy heuristic is to construct a solution from scratch (the empty set. choosing at each step the item bringing the "best" immediate reward" [1]. This holds true for the ship travel example of the “Research on Ship Meteorological Route Based on A-Star Algorithm” study where an empty set was initialized and a greedy algorithm was first found based on a shortest distance heuristic from the goal. The solution was then improved upon through recursion or a feasible solution is not found. The heuristic is the other part of A* algorithm derived from a greedy search with a proper heuristic properly defining the cost between the nodes. "Integer Programming" states this by stating "Greedy heuristic have to be adapted to the particular structure. For [shortest-path problems] there are several possible greedy heuristics that choose edge one after another until a tour is obtained." [1]. This use of a heuristic can be seen in all other application of A* in shortest path problems where a path is found through a heuristic determined by distance of node from the goal.
Pseudo code example of A* algorithm built of greedy algorithm:
open_list, closed_list = empty list of possible positions
adjacent_value=0
next_position=null
push start_position to open_list
while open_list is not empty
current node = pop open_list
for each adjacent position of current_node (ap_current) with value (av_current)
if adjacent_value is less than av_current or ap_current is in closed_list
adjacent_value= av_current
next_position= ap_current
push ap_current to closed_list
push next_position to open_list
An early study of the algorithm was done in “A Comparative Study of A-Star Algorithms for Search and Rescue in Perfect Maze” by Xiang Liu and Daoxiong Gong of Beijing University of Technology in 2011 where the algorithm was used to track the fastest path through a maze. Three A* Algorithms were used with different heuristics based on Euclidian distance, Euclidian distance from start and from base of current path and angle from current position to the goal shown in variations of the standard A* Algorithm:
Variation 1: is the position, is the cost from the start point to the current position and is the Euclidian distance to the target
Variation 2: is the position, is the cost from the start point to the current position and is the Euclidian distance to the target point and the Euclidian distance to the parent point of this branch
Variation 3: where is a weight, is the Euclidian distance, is the angle from the starting point to the current position and is the angle from the ending point to the current position [2]
On all occasions at least one of the A* Algorithms out performed a depth search with the second heuristic performing the best "generally, in unknown maze, while only proximate location of target point is known, A∗ algorithm is better than depth-first search algorithm in searching, however when the heuristic functions are different, searching results are also different." [2] Figure 1 shows the results of the maze experiment using 10 perfect randomly generated mazes.
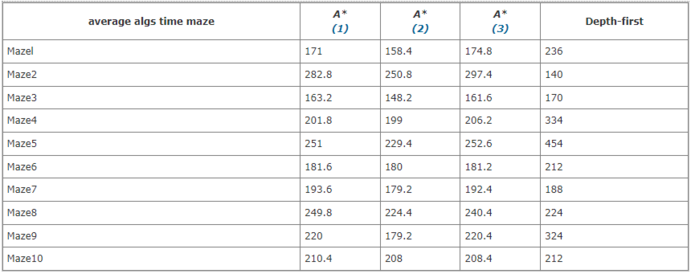
Many discussions exist revolving the best use of the A* Algorithm and also where it is most highly utilized. One of them being the game industry, mainly used to find the shortest path. There is a plethora of shortest path algorithms but A* is one of the preferred methods.[3] A* Algorithm is an implementation of heuristic search, a process that will give an estimation value from current node to goal node. This implementation will always find the smallest value optimal path using:
where is a node, is the distance from starting node to node, and
is a heuristic value of estimation distance from node n to finish node.[3]
One of the methods of using the A* Algorithm in the gaming industry is when creating automated movement for non-playable characters, the challenge being that they need to move in a realistic way. The combination of using a hexagon based environment versus a grid based environment is one of the discussions seen today.
Numerical Example
The A* Algorithm is a great approach for finding the lowest-cost path between two points. In the Figure 2, we are seeking to find the shortest distance between two nodes.
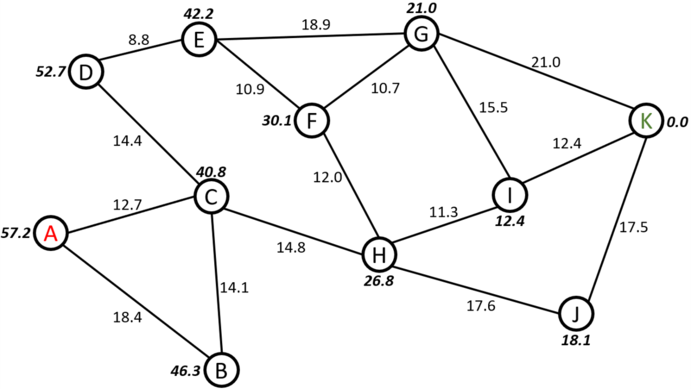
The above image is a representation of mapped locations. Each node is a location, and the lines between the nodes is the path between their respective nodes. The numbers on the paths are the distance between each node, g(n). The numbers next to each node represents the straight-line distance between their respective node and the objective node, h(n), and these shall be our heuristic value. Here, the objective is to find the shortest path between our starting node, Node A, and our objective node, Node K. Thus, the A* algorithm will be employed below, where f(n) is the objective function.
Below, steps are outlined for how the objective function is executed.
Starting from Node A, Node C or Node B can be chosen; by applying the A* Algorithm below, the best path can be chosen.
Step 1: For Node B, the heuristic value, , is 46.3, and it is added to the parameter, , which is 18.4.
Step 2: For Node C, the heuristic value, , is 40.8, and it is added to the parameter, , which is 12.7.
Step 3: Since yields the smaller value, this value is chosen as taking the path between Node A and Node C. This path is highlighted yellow in Figure 3.
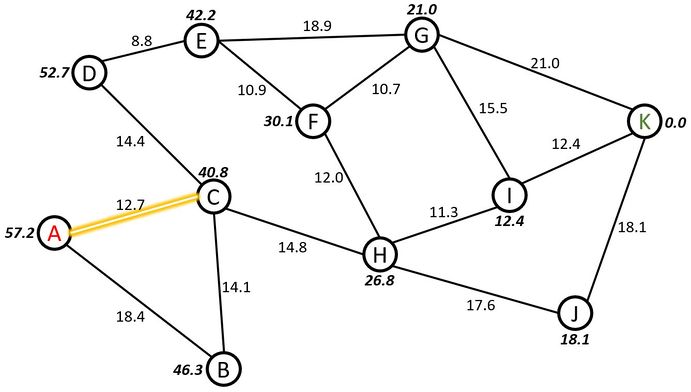
Now, the A* algorithm is employed to chose the next path from Node C. Here, Node D or Node H can be chosen.
Step 4: For Node D, the heuristic value, , is 52.7, and it is added to the sum of the parameters, , which is the sum of the path distance value from Nodes A to C, 12.7, with the path distance value from Nodes C to D, 14.4.
Step 5: For Node H, the heuristic value, , is 26.8, and it is added to the sum of the parameters, , which is the sum of the path distance value from Nodes A to C, 12.7, with the path distance value from Nodes C to H, 14.8.
Step 6: Since yields a smaller value, this value is chosen as taking the path between Nodes C to H. The path is highlighted yellow in Figure 4.
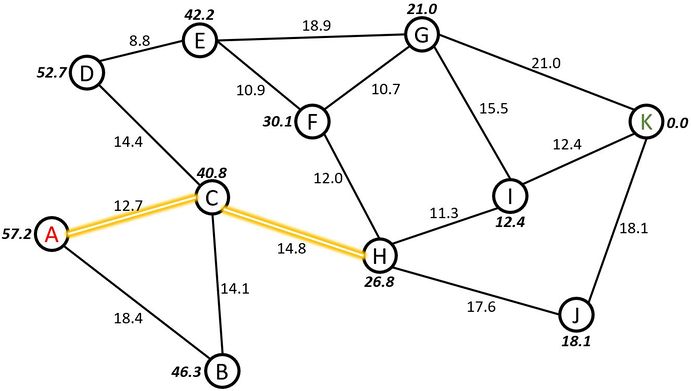
Next step applies A* algorithm from Node H to either Nodes I or J.
Step 7: For Node I, the heuristic value, , is 12.4, and it is added to the sum of the parameters, , which is the sum of the path distance values from Nodes A to H, 12.7 and 14.8, respectively, with the path distance value from Nodes H to I, 11.3.
Step 8: For Node J, the heuristic value, , is 18.1, and it is added to the sum of the parameters, , which is the sum of the path distance values from Nodes A to H, 12.7 and 14.8, respectively, with the path distance value from Nodes H to J, 17.6.
Step 9: Since yields a smaller value, this value is chosen as taking the path from Nodes H to I. The path continues to be highlighted yellow in Figure 5.
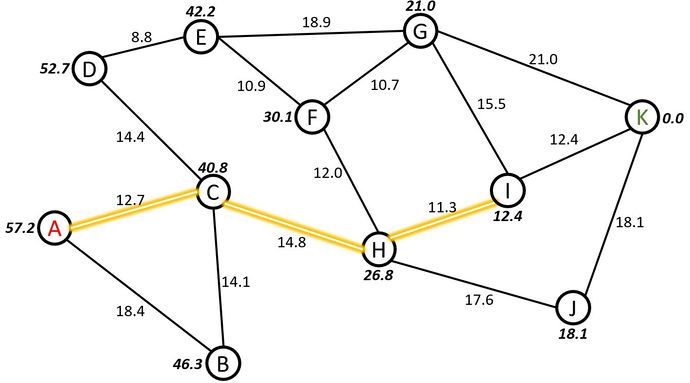
Next step applies A* algorithm from Node I to either Nodes G or K.
Step 10: For Node G, the heuristic value, , is 21.0, and it is added to the sum of the parameters, , which is the sum of the path distance values from Nodes A to I, 12.7, 14.8, and 11.3, respectively, with the path distance value from Nodes I to G, 15.5.
Step 11: For Node K, the heuristic value, , is 0.0, and it is added to the sum of the parameters, , which is the sum of the path distance values from Nodes A to I, 12.7, 14.8, and 11.3, respectively, with the path distance value from Nodes I to K, 12.4.
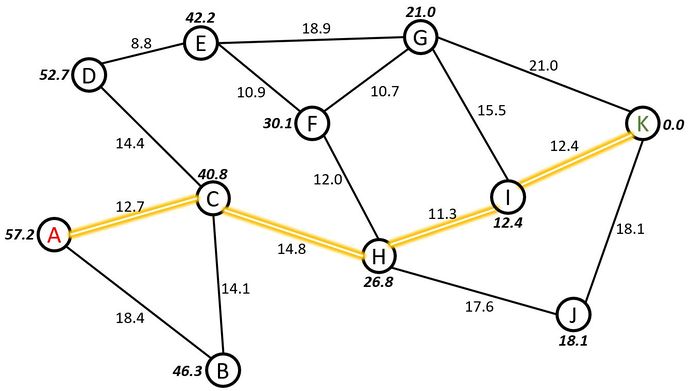
Since is the smaller value, and K is the objective Node, the A* Algorithm has found the shortest path between Nodes A and K. The path is highlighted in Figure 6.
Application
Public Transportation in Cities
Optimal routes are essential in creating successful transportation systems. Transportation systems affect entire societies and their quality of life. Minimizing transportation time and distance, effectively reduces time spent traveling, traffic, risk of death or injury while traveling, air pollution and costs incurred from traveling. Transportation is also considered a barrier to impoverished communities, affecting access to employment and other essential services, directly impacting economies. The objective of applying the A* algorithm to transportation challenges is to minimize cost and travel time for transportation.
An analysis was conducted on the transportation system in Yangon, Myanmar[4]. Public transportation in the Yangon area is prevalent and the preferred method of transportation is public transportation. In this study, the bus routes were utilized to construct the algorithm to determine shortest paths in their transportation network. Bus stops were represented through nodes and bus lines were the links between those nodes.
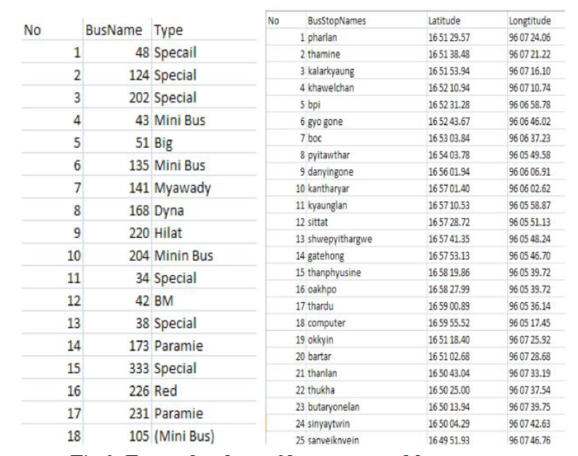
The approach to analysis with the implementation of the A* algorithm was similar to our initial approach. This proposed system in the Yangon area focused solely on the distance between nodes. To improve efficiency, an algorithm that includes data and analysis on traffic patterns, road closures and wait times for bus stops would aid users in optimizing their transportation selection. The use of the A* algorithm bus network in a region so heavily reliant on public transportation is a respectable strategy to address transportation concerns in the Yangon area.
Pathfinding in Video Games
Pathfinding algorithms are increasingly used in video game development globally. Artificial Intelligence issues are prevalent as these games increase in complexity. Decision-making, movements and strategy are instances where pathfinding algorithms, such as the A* algorithm, are utilized to find optimal solutions. In video games where users make decisions, path finding may increase with complexity as decisions are dynamic according to the user's input. Pathfinding uses up CPU power and memory. The objective is to optimize paths between characters and their endpoints to minimize CPU power and memory used to maximize game performance.
Conclusion
Through the use of a serpentine node map system, using each road and intersection as an edge and node respectively and scoring each based on our characteristics, a basis was built on which to run the A* algorithm. The algorithm was then able to traverse the map finding the shortest, fastest, and most fuel-efficient path in order to minimize the inconvenience to the traveler and the environmental impact. Through the A* algorithm on the node map travel can be optimized to be more efficient and faster for both commercial and pedestrian travel.
References
- ↑ 1.0 1.1 L.A. Wolsey, Integer Programming. Wiley, 1998.
- ↑ 2.0 2.1 2.2 Liu, Xiang, and Gong, Daoxiong. “A Comparative Study of A-Star Algorithms for Search and Rescue in Perfect Maze.” 2011 International Conference on Electric Information and Control Engineering, 2011, https://doi.org/10.1109/iceice.2011.5777723.
- ↑ 3.0 3.1 P. O. N. Saian, Suyoto and Pranowo, "Optimized A-Star algorithm in hexagon-based environment using parallel bidirectional search," 2016 8th International Conference on Information Technology and Electrical Engineering (ICITEE), pp. 1-5, 2016, https://doi.org/10.1109/ICITEED.2016.7863246.
- ↑ Zar, Myat Thu and Sein, Myint Myint. “Using A* Algorithm For Public Transportation System in Yangon Area.” 2015 International Journal of Advanced Computational Engineering and Networking, vol. 3, issue 3, pp. 7 –10























