Bayesian Optimization: Difference between revisions

From Cornell University Computational Optimization Open Textbook - Optimization Wiki
Jump to navigation Jump to search
VisualWikitext
No edit summary
Line 26: Line 26:
<math> E[f[x]] - m[x] </math>
<math> E[f[x]] - m[x] </math>


<math> E[(f[x]−m[x]) </math> <math>(f[x′]−m[x′])] </math> = <math> k[x, x′] </math>
<math> E[(f[x]−m[x]) (f[x\prime]−m[x\prime])] = k[x, x\prime] </math>


Given observations <math> f= [f[x_1],f[x_2],\dotsc,f[x_t]] </math> at <math> t </math> points, we would like to make a prediction about the function value at a new point <math> x^\star </math>. This new function value <math>f^\star=f[x^\star]</math> is jointly normally distributed with the observations <math> f </math> so that:
Given observations <math> f= [f[x_1],f[x_2],\dotsc,f[x_t]] </math> at <math> t </math> points, we would like to make a prediction about the function value at a new point <math> x^\star </math>. This new function value <math>f^\star=f[x^\star]</math> is jointly normally distributed with the observations <math> f </math> so that:
Line 78: Line 78:
  6:    '''end for'''
  6:    '''end for'''


==Applications==
== Applications==
Bayesian Optimization has shown a wide variety of interest in areas of data science and Chemical Engineering, Material Science domain. Some of the applications are stated below:
Bayesian Optimization has shown a wide variety of interest in areas of data science and Chemical Engineering, Material Science domain. Some of the applications are stated below:


Line 87: Line 87:
*'''Materials''' - Bayesian Optimization is applied to design experiments of previous experiments to suggest features of the new materials whose performance is evaluated by simulation. Final goal is to improvise the design while reducing the number of experimentation. Bayesian Optimization are used to predict compounds with low thermal conductivity <ref>https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/201594/1/PhysRevLett.115.205901.pdf</ref>, optimal melting temperature <ref>https://arxiv.org/pdf/1310.1546.pdf</ref>, elastic properties<ref>https://www.nature.com/articles/ncomms11241/bay</ref>
*'''Materials''' - Bayesian Optimization is applied to design experiments of previous experiments to suggest features of the new materials whose performance is evaluated by simulation. Final goal is to improvise the design while reducing the number of experimentation. Bayesian Optimization are used to predict compounds with low thermal conductivity <ref>https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/201594/1/PhysRevLett.115.205901.pdf</ref>, optimal melting temperature <ref>https://arxiv.org/pdf/1310.1546.pdf</ref>, elastic properties<ref>https://www.nature.com/articles/ncomms11241/bay</ref>


==Example ==
==Example==
Here using the HyperOpt package <ref>http://hyperopt.github.io/hyperopt/</ref>; a simple optimization problem will be solved: The example is broken down into four steps <ref>https://github.com/WillKoehrsen/hyperparameter-optimization/blob/master/Introduction%20to%20Bayesian%20Optimization%20with%20Hyperopt.ipynb</ref>:
Here using the HyperOpt package <ref>http://hyperopt.github.io/hyperopt/</ref>; a simple optimization problem will be solved: The example is broken down into four steps <ref>https://github.com/WillKoehrsen/hyperparameter-optimization/blob/master/Introduction%20to%20Bayesian%20Optimization%20with%20Hyperopt.ipynb</ref>:


Line 97: Line 97:
[[File:ObjectiveFunction.png|none|frame|Objective Function where the minimum occurs at x = 4.8779]]
[[File:ObjectiveFunction.png|none|frame|Objective Function where the minimum occurs at x = 4.8779]]


=== Domain ===
===Domain===
The domain is the value of x over which we evaluate this function. We can use a uniform distribution in our case over the space of function is defined.
The domain is the value of x over which we evaluate this function. We can use a uniform distribution in our case over the space of function is defined.


=== Run the Optimization ===
===Run the Optimization===
In order to run the optimization; 2000 runs of the minimization with the Tree Parzen Estimator Algorithm is done. The function fmin, as shown in the figure below; takes in exactly four parts; the objective, total number of runs, algorithm, and the trials.  The final result is printed as 4.8748151906. Hence reaching the optima.
In order to run the optimization; 2000 runs of the minimization with the Tree Parzen Estimator Algorithm is done. The function fmin, as shown in the figure below; takes in exactly four parts; the objective, total number of runs, algorithm, and the trials.  The final result is printed as 4.8748151906. Hence reaching the optima.
[[File:Hyperparameter optiomizatin.jpg|none|thumb|389x389px|Code for Bayesian Optimization]]
[[File:Hyperparameter optiomizatin.jpg|none|thumb|389x389px|Code for Bayesian Optimization]]


=== Results: ===
===Results:===
From the results we can see that overtime the algorithm tends to values closer to our original global optimization solution of 4.9, but the points tend to cluster around the actual minimum as the algorithm progresses.
From the results we can see that overtime the algorithm tends to values closer to our original global optimization solution of 4.9, but the points tend to cluster around the actual minimum as the algorithm progresses.
[[File:X values aftereach ieration.png|left|thumb|Results After each Iteration]]
[[File:X values aftereach ieration.png|left|thumb|Results After each Iteration]]
Line 153: Line 153:
|-
|-
|PyBO
|PyBO
|BSD
| BSD
|https://github.com/mwhoffman/pybo
|https://github.com/mwhoffman/pybo
|Python
|Python
Line 165: Line 165:
|}
|}


==Conclusion ==
==Conclusion==
In conclusion <ref>https://towardsdatascience.com/an-introductory-example-of-bayesian-optimization-in-python-with-hyperopt-aae40fff4ff0</ref>; Bayesian Optimization primarily is utilized when Blackbox functions are expensive to evaluate and are noisy, and can be implemented easily in Python {HyperOpt, Spearmint, PyBO, MOE}.  Bayesian optimization uses a surrogate function to estimate the objective through sampling. These surrogates {Gaussian Process} are represented as probability distributions which can be updated in light of new information. The Acquisition functions {Upper Bound Confidence, Probability of Improvement, Expected Improvement} then are used to evaluate the probability of exploring a certain point in space will yield a good return. Lastly Bayesian optimization is often extended to complex problems including and not limited to hyperparameter tuning of machine learning models.
In conclusion <ref>https://towardsdatascience.com/an-introductory-example-of-bayesian-optimization-in-python-with-hyperopt-aae40fff4ff0</ref>; Bayesian Optimization primarily is utilized when Blackbox functions are expensive to evaluate and are noisy, and can be implemented easily in Python {HyperOpt, Spearmint, PyBO, MOE}.  Bayesian optimization uses a surrogate function to estimate the objective through sampling. These surrogates {Gaussian Process} are represented as probability distributions which can be updated in light of new information. The Acquisition functions {Upper Bound Confidence, Probability of Improvement, Expected Improvement} then are used to evaluate the probability of exploring a certain point in space will yield a good return. Lastly Bayesian optimization is often extended to complex problems including and not limited to hyperparameter tuning of machine learning models.


==References==
==References==
<references />
<references />

Revision as of 15:26, 28 November 2021

Author : By Deepa Korani (dmk333@cornell.edu)

Steward : Fenqgi You

Introduction

Bayesian Optimization is a sequential model-based approach to solving problems. In particular, it prescribes a prior belief over the possible objective functions, and then sequentially refine the model as data are observed via Bayesian posterior updating. [1]

Bayesian Optimization is useful in machine learning. Since Machine Learning consists of black box optimization problem where the objective function is a black box function[2], and the analytical expression for the function is unknown. Bayesian optimization can be useful here. They attempt to find the global optimum in a minimum number of steps.

Bayesian Optimization has shown tremendous solutions for a wide variety of design problems. Certain application include; robotics, environmental monitoring, combinatorial optimization, adaptive Monte Carlo, reinforcement learning. [3]

Methodology and Algorithm

Methodology

Bayesian Optimization Algorithm has two main components:

Probabilistic Model:[4]

The other word for the probabilistic model is called as the surrogate function or the posterior distribution. The posterior captures the updated belief about the unknown objective function. A better interpretation of this is to estimate the objective the function with a surrogate function. Common Surrogate function used to model is the Gaussian Process (GP). Other probabilistic models are Random Forests[5], and Tree Parzen Estimators [6].

Here in the Gaussian Process will be described in detail:

Gaussian Process[GP]:

Gaussian Process can be described as a collection of random variables, where any finite number of these are jointly normally distributed. It is defined by a mean function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m[x] } and a covariance function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k[x,x'] } that returns similiarity among two points. The Gaussian process models the objective function as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f[x] \sim GP[m[x],k[x,x']] } we are saying that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E[f[x]] - m[x] }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E[(f[x]−m[x]) (f[x\prime]−m[x\prime])] = k[x, x\prime] }

Given observations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f= [f[x_1],f[x_2],\dotsc,f[x_t]] } at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t } points, we would like to make a prediction about the function value at a new point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^\star } . This new function value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^\star=f[x^\star]} is jointly normally distributed with the observations Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } so that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Pr([ff∗])=Norm[0,[K[X,X]K[X,x∗]K[x∗,X]K[x∗,x∗]]] }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K[X,X] } is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\times t } matrix where element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i,j) } is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k[xi,xj], K[X,x^\star] } is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\times 1 } vector where element Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i } is given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k[x_i,x^\star] } and so on.

Since the function values in equation above are jointly normal, the conditional distribution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Pr(f^\star \vert f) } must also be normal, and we can use the standard formula for the mean and variance of this conditional distribution:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Pr(f^\star \vert f)=Norm[\mu [x^\star], \sigma^2 [x^ \star]] }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu[x^\star] } = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K[x^\star,X] } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [K[X,X]]^{−1} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2[x^\star] } =Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K[x^\star,x^\star] } − Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K[x^\star,X] } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [K[X,X]]^{-1}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K[X,x^\star] }

Using this formula, we can estimate the distribution of the function at any new point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\star } . The best estimate of the function value is given by the mean Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu[x] } , and the uncertainty is given by the variance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma^2[x] } .

Acquisition Function: [7]

The role of the acquisition function is to guide the search for the optimum. Typically, acquisition functions are defined such that high acquisition corresponds to potentially high values of the objective function, whether because the prediction is high, the uncertainty is great, or both. Maximizing the acquisition function is used to select the next point at which to evaluate the function. That is, we wish to sample ƒ at argmaxxu(x|D), where u(·) is the generic symbol for an acquisition function.

A good acquisition function should trade off exploration and exploitation. A quick section of common acquisition functions are defined below:

Error creating thumbnail: File with dimensions greater than 12.5 MP
Four different Acquisition functions [8]
Upper Bound Confidence:

This acquisition function is defined as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle UCB[x^\star] } = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu[x^\star] } + Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta^{1/2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma[x*] }

Probability of Improvement:

This acquisition function computes the likelihood that the function at x∗ will return a result higher than the current maximum f[^x]. For each point x∗, we integrate the part of the associated normal distribution that is above the current maximum (figure 4b) so that:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle PI[x^\star] } = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{f[x]}^{\infty} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Norm_{f[x^\star]}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mu[x^\star]],\sigma[x^\star]]} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df[x^\star]}

Expected Improvement:

The expected Improvement can be model as:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle EI[x^\star] } = Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{f_[\hat{x}]}^{\infty} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f[x^\star]-f[\hat{x}]) } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Norm_{f[\hat{x}]}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\mu[x^\star],\sigma[x^\star]] } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df[x^\star] }

Algorithm [9]

Here follows a longer example of mathematical-style pseudocode, for the Bayesian Optimization: 

1: Algorithm' Bayesian Optimization ' is
2:    for t == 1,2,.....do  
3:         Find xt by optimizing the the acquisition function over the GP: xt = argmaxxu(x|D1:t-1)
4:         Sample the objective function yt = f(xt) + εt
5:         Augment the data D1:t = {D1:t-1,(xt,yt)} and update the GP
6:    end for

Applications

Bayesian Optimization has shown a wide variety of interest in areas of data science and Chemical Engineering, Material Science domain. Some of the applications are stated below:

  • A/B Testing - Though the idea of A/B testing dates back to the early days of advertising in the form of so-called focus groups, the advent of the internet and smartphones has given web and app developers a new forum for implementing these tests at unprecedented scales. By redirecting small fractions of user traffic to experimental designs of an ad, app, game, or website, the developers can utilize noisy feedback to optimize any observable metric with respect to the product’s configuration. In fact, depending on the particular phase of a product’s life, new subscriptions may be more valuable than revenue or user retention, or vice versa; the click-through rate might be the relevant objective to optimize for an ad, whereas for a game it may be some measure of user engagement. The crucial problem is how to optimally query these subsets of users in order to find the best product with high probability within a predetermined query budget, or how to redirect traffic sequentially in order to optimize a cumulative metric while incurring the least opportunity cost.
  • Recommender Systems - Generally Recommender systems are used by online content providers to recommend products to their subscribers. Recommending the right product to subscribers is important in order to improvise the revenue in case for e-commerce sits, or consumption sites.
  • Natural Language Processing and Text- Bayesian Optimization has been applied to improve text extraction. [10]
  • Environmental Monitoring and Sensor Networks - Sensor Networks allow monitoring important environment conditions; such as temperature, concentration of pollutants in the atmosphere, soil and ocean. These networks make noise measurements that are interpolated to produce a global model of interest. In some cases, these sensors are expensive to activate but one can answer important questions like what is the hottest or coldest spot in a building by activating a relatively small number of sensors. Bayesian optimization was used for this task and the similar one of finding the location of greatest highway traffic congestion [11]
  • Materials - Bayesian Optimization is applied to design experiments of previous experiments to suggest features of the new materials whose performance is evaluated by simulation. Final goal is to improvise the design while reducing the number of experimentation. Bayesian Optimization are used to predict compounds with low thermal conductivity [12], optimal melting temperature [13], elastic properties[14]

Example

Here using the HyperOpt package [15]; a simple optimization problem will be solved: The example is broken down into four steps [16]:

Objective Function

The objective function for this example is a simple function that is defined that returns the value that needs to be minimized.

A simple objective is used that returns a single real value number to minimize. The code to plot the objective function was written in python.

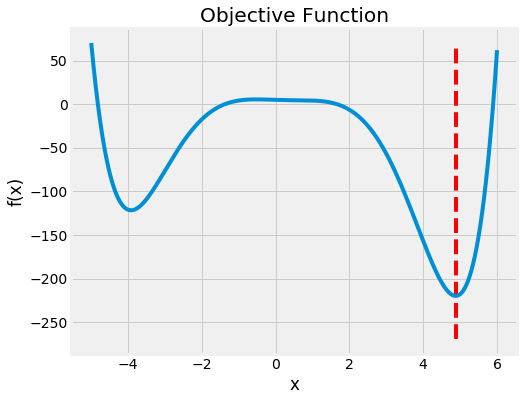
Objective Function where the minimum occurs at x = 4.8779

Domain

The domain is the value of x over which we evaluate this function. We can use a uniform distribution in our case over the space of function is defined.

Run the Optimization

In order to run the optimization; 2000 runs of the minimization with the Tree Parzen Estimator Algorithm is done. The function fmin, as shown in the figure below; takes in exactly four parts; the objective, total number of runs, algorithm, and the trials. The final result is printed as 4.8748151906. Hence reaching the optima.

Code for Bayesian Optimization

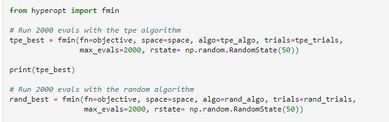
Results:

From the results we can see that overtime the algorithm tends to values closer to our original global optimization solution of 4.9, but the points tend to cluster around the actual minimum as the algorithm progresses.

Results After each Iteration






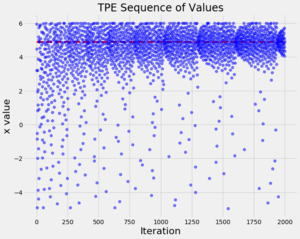
Bayesian Optimization Packages

Here are a list of packages in Python, Java, C++that utelize Bayesian Optimization

Table - Packages Utilizing Bayesian Optimization [17]
Package License URL Language Model
SMAC Academic http://www.cs.ubc.ca/labs/beta/Projects/SMAC Java Random Forest
Hyperopt BSD https://github.com/hyperopt/hyperopt Python Tree Parzen Estimator
Spearmint Academic https://github.com/HIPS/Spearmint Python Gaussian Process
Bayesopt GPL https://github.com/rmcantin/bayesopt C++ Gaussian Process
PyBO BSD https://github.com/mwhoffman/pybo Python Gaussian Process
MOE Apache 2.0 https://github.com/Yelp/MOE Python/ C++ Gaussian Process

Conclusion

In conclusion [18]; Bayesian Optimization primarily is utilized when Blackbox functions are expensive to evaluate and are noisy, and can be implemented easily in Python {HyperOpt, Spearmint, PyBO, MOE}. Bayesian optimization uses a surrogate function to estimate the objective through sampling. These surrogates {Gaussian Process} are represented as probability distributions which can be updated in light of new information. The Acquisition functions {Upper Bound Confidence, Probability of Improvement, Expected Improvement} then are used to evaluate the probability of exploring a certain point in space will yield a good return. Lastly Bayesian optimization is often extended to complex problems including and not limited to hyperparameter tuning of machine learning models.

References

  1. ↑ http://krasserm.github.io/2018/03/21/bayesian-optimization/
  2. ↑ https://arxiv.org/abs/1012.2599
  3. ↑ https://dash.harvard.edu/bitstream/handle/1/27769882/BayesOptLoop.pdf;sequence=1
  4. ↑ https://arxiv.org/pdf/1012.2599.pdf
  5. ↑ https://www.cs.ubc.ca/~hutter/papers/10-TR-SMAC.pdf
  6. ↑ https://proceedings.neurips.cc/paper/2011/file/86e8f7ab32cfd12577bc2619bc635690-Paper.pdf
  7. ↑ https://arxiv.org/pdf/1012.2599.pdf
  8. ↑ https://www.borealisai.com/en/blog/tutorial-8-bayesian-optimization/
  9. ↑ https://arxiv.org/pdf/1012.2599.pdf
  10. ↑ https://arxiv.org/pdf/1402.7005.pdf
  11. ↑ https://arxiv.org/pdf/0912.3995.pdf
  12. ↑ https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/201594/1/PhysRevLett.115.205901.pdf
  13. ↑ https://arxiv.org/pdf/1310.1546.pdf
  14. ↑ https://www.nature.com/articles/ncomms11241/bay
  15. ↑ http://hyperopt.github.io/hyperopt/
  16. ↑ https://github.com/WillKoehrsen/hyperparameter-optimization/blob/master/Introduction%20to%20Bayesian%20Optimization%20with%20Hyperopt.ipynb
  17. ↑ https://dash.harvard.edu/bitstream/handle/1/27769882/BayesOptLoop.pdf;sequence=1
  18. ↑ https://towardsdatascience.com/an-introductory-example-of-bayesian-optimization-in-python-with-hyperopt-aae40fff4ff0
Retrieved from "https://optimization.cbe.cornell.edu/index.php?title=Bayesian_Optimization&oldid=4215"