Disjunctive inequalities

Introduction

Disjunctive inequalities are a form of disjunctive constraints that can be applied to linear programming. Disjunctive constraints are applied in all disjunctive programming, which just refers to the use of logical constraints, which include the “Or” and “And” statements. In order to solve a disjunctive, the constraints have to be converted into multiple integer programming (MIP) constraints, which is called disjunction. Disjunction involves the implementation of a binary variable to create a new set of constraints that can be solved easily. Two common methods for disjunction are the Big-M Reformulation and the Convex-Hull Reformulation.

Method

General

When given a set of inequalities, such as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1(x)\ \le\ 0\ \And \ f_2(x)\ \le\ 0 } , the disjunctive form is given by:  Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} y \\ f_1(x)\ \le\ 0 \end{bmatrix} \lor \begin{bmatrix} -y \\ f_2(x)\ \le\ 0 \end{bmatrix} } . In order to turn the problem into a solvable MIP or MILP, logical constraints are created by using sufficiently large numbers, such as M1 and M2, and a binary variable y for each inequality. This is shown below by M1, M2, y1, and y1:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1(x)\ \le\ M_1\ast(1-y_1)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_2(x)\ \le\ M_2\ast(1-y_2)}

To set the binary variable to be mutually exclusive, the sum of the variables is set to 1 and the range is set to {0,1}.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1\ +y_2\ =\ 1 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1\ ,\ y_2\epsilon\ {0,1}\ \ }

Big-M Reformulation

Figure 1: Disjunctive inequality solution space that can be solved via disjunction using the Big-M Reformulation or the Convex-Hull Reformulation

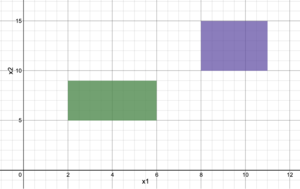
For the Big-M reformulation, a sufficiently large number, M, is used to nullify one set of constraints. This is accomplished by adding or subtracting the term “M*(1-y)” to the upper bound and lower bound constraints, respectively, with its respective binary variable. For example, given a solution space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} y \\ 2\le\ x_1\ \le6 \\ 5\le\ x_2\ \le9 \end{bmatrix} \lor \begin{bmatrix} -y \\ 8\le\ x_1\ \le11 \\ 10\le\ x_2\ \le15\ \end{bmatrix} } (shown graphically in Figure 1), to determine which of the solutions is optimal, the problem must be formulated such that one set of constraints is chosen. Using the Big-M Reformulation, the following MILP set would be obtained:

y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 - M*(1-y_1) \leq x1 \leq 6 + M*(1-y_1)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5 - M*(1-y_1) \leq x2 \leq 9 + M*(1-y_1) }

-y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8 - M*(1-y_2) \leq x1 \leq 11 + M*(1-y_2)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10 - M*(1-y_2) \leq x2 \leq 15 + M*(1-y_2)}

Convex-Hull Reformulation

Similar to the Big-M reformulation, the convex-hull reformulation uses a binary variable, y, to constrain the set of inequalities. The first step in converting the problem into a solvable MILP is breaking all variables into a set of variables, such as (x1 → x11 + x12). By adding these addition variables, it is possible to isolate what set of parameters provide for the optimal solution of the problem. Then, similar to the Big-M reformulation, a sufficiently large variable, M, is used to nullify the non-optimal variable set, such as x11 and x12. For the problem show in Figure 1, the following variable constraints would be formulated:

y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq x_{11} \leq M*y_1 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq x_{21} \leq M*y_1}

-y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq x_{12} \leq M*y_2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq x_{22} \leq M*y_2}

Formulation of the numerical constraints would then be implemented: y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\ast y_1\le\ x_{11}\ \le6\ast y_1 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5\ast y1\le\ x_{21}\ \le9\ast y1}

-y Formulation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8\ast y_2\le\ x_{12}\ \le11\ast y_2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10\ast y_2\le\ x_{22}\ \le15\ast y_2}

With the Convex-Hull transformation, the additional constraints confine the problem, such that a tighter (convex) solution space is examined compared to Big-M Formulation.

References

Authors: Daniel Ladron, Grant Logan, Matthew Dinh, Derek Moore (CBE/SysEn 6800, Fall 2021)