Frank-Wolfe: Difference between revisions
| Line 181: | Line 181: | ||
'''Step 1. Utilize new iteration point as the starting point ''' | '''Step 1. Utilize new iteration point as the starting point ''' | ||
From ''Step 4'', <math> x_1 = [1,1]</math>. | From ''Step 4'' in ''Iteration 1'', <math> x_1 = [1,1]</math>. | ||
Therefore, substituting <math>x_1</math> into <math>\delta f_x(x,y)</math> and <math>\delta f_y(x,y)</math> from ''Step 1'', | Therefore, substituting new iteration point <math>x_1</math> into <math>\delta f_x(x,y)</math> and <math>\delta f_y(x,y)</math> from ''Step 1'', | ||
<math display="block">\nabla f(1,1) = z_1 = [0, 0] </math> | <math display="block">\nabla f(1,1) = z_1 = [0, 0] </math> | ||
Revision as of 04:43, 11 December 2021
Author: Adeline Tse, Jeff Cheung, Tucker Barrett (SYSEN 5800 Fall 2021)
Introduction
The Frank-Wolfe algorithm is an iterative first-order optimization algorithm for constrained convex optimization, first proposed by Marguerite Frank and Philip Wolfe from Princeton University in 1956.[1] It is also known as the “gradient and interpolation” algorithm or sometimes the “conditional gradient method” as it utilizes a simplex method of comparing an initial feasible point with a secondary basic feasible point to maximize the linear constraints in each iteration to find or approximate the optimal solution.
Advantages of the Frank-Wolfe algorithm include that it is simple to implement, it results in a projection-free computation (that is, it does not require projections back to the constraint set to ensure feasibility), and it generates solution iterations that are sparse with respect to the constraint set. However, one of the major drawbacks of Frank-Wolfe algorithm is the practical convergence, which can potentially be an extremely slow computation process. Nonetheless, new sub-method has been proposed to accelerate the algorithm by better aligning the descent direction while still preserving the projection-free property. [2] Therefore, despite the downside of Frank-Wolfe algorithm, the numerous benefits of this algorithm allow it to be utilized in artificial intelligence, machine learning, traffic assignment, signal processing, and many more applications.
Theory & Methodology
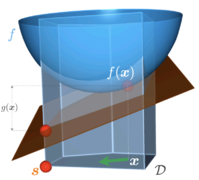
The Frank-Wolfe algorithm uses step size and postulated convexity, which formulates a matrix of positive semidefinite quadratic form. Just like a convex function yields a global minimum at any local minimum on a convex set, by the definition of nonlinear programming, the concave quadratic function would yield a global maximum point at any local maximum on a convex constraint set.
The methodology of the Frank-Wolfe algorithm starts with obtaining the generalized Lagrange multipliers for a quadratic problem, PI. The found multipliers are considered solutions to a new quadratic problem, PII. The simplex method is then applied to the new problem, PII, and the gradient and interpolation method is utilized to make incremental steps towards the solution of the original quadratic problem, PI. This is performed by taking an initial feasible point, obtaining a second basic feasible point along the gradient of the objective function at the initial point, and maximizing the objective function along the segment that joins these two points. The found maximum along the segment is utilized as the starting point for the next iteration.[1] Using this method, the values of the objective function converge to zero and in one of the iterations, a secondary point will yield a solution.
Proof
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times 1]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [m \times n]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} is a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times n]} matrix
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b} are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [1 \times n]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [1 \times m]} matrices respectively
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x)} is the gradient
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = \sum_{j=1}^n p_jx_j - \sum_{j,k=1}^{n,n} X_jC_{jk}X_k} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle where \; \sum_{j=1}^n A_{ij}X_j \le b_i \quad (i=1, ..., m) \; and \; X_j \ge 0 \quad (j = 1, ..., n)}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x) = \frac{df(x)}{dx}}
PI is represented by the following equations using matrix notation:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Maximize} \qquad f(x) = px' - x'Cx \quad \text{subject to}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (I) = \begin{cases} x \ge 0 \\ Ax \le b \end{cases}}
Since PI is feasible, any local maximum found that is contained within the convex constraint set is a global maximum. Then by utilizing Kuhn and Tucker's generalizations of the Lagrange Multipliers of the maximization of the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} is considered the solution of PI.
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x_0)x_0 = Max \, [ \, \delta f(x_0)w \, | \, w \ge 0, Aw \le b], \quad where \; w \; \text{is an} \; [n \times 1] \; \text{matrix}}
By the Duality Theorem, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Min \, [ \, ub \, | \, u \ge 0, \, uA \ge \delta f(x_o)], \quad where \; u \; \text{is a} \; [1 \times m] \; \text{matrix}}
Therefore, the solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} for PI is only valid if: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Max \, [ \, \delta f(x_0)x_0 - ub \, | \, u \ge 0, uA \ge \delta f(x_0)] = 0}
Since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x) = p - 2x'Cx} Therefore, by the generalization of Lagrangian, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u)} is extracted with linear constraints: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) = \delta f(x)x - ub = px - ub - 2x'Cx} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{cases} x \ge 0, \quad u \ge 0,\\ Ax \le b, \quad \delta f(x) \le uA \end{cases}}
The completion of the generalized Lagrangian shows that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m + n} positive variables exist for PI, thus a feasible solution exists.
Based on the concavity of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le \delta f(x)(y-x)}
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,u)} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) \le 0} (where x is a solution if for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u, \; g(x,u)=0} ), then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le \delta f(x)x \le uAy - \delta f(x)x \le ub - \delta f(x)x = -g(x,u)}
By the Boundedness Criterion and the Approximation Criterion, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(y) - f(x) \le -g(x,u)}
The Frank-Wolfe algorithm then adds a non-negative variable to each of the inequalities to obtain the following:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu} are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [m \times 1]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [n \times 1]} matrices respectively
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x, \, u, \, y, \, \nu \ge 0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax+y=b} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2Cx+A'u'-\nu '=p'} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x,u) = \delta f(x)x-ub = (uA-\nu )x-u(Ax+y) = - \nu x + uy}
Thus, the PII problem is to obtain search vectors to satisfy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu x+uy=0} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is considered a solution of PI if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f(x)} belongs to the convex cone spanned by the outward normals to the bounding hyperplanes on which Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} lines as shown in Figure 1.
Algorithm
The Frank-Wolfe algorithm can generally be broken down into five steps as described below. Then the loop of iterations continues throughout Step 2 to Step 5 until the minimum extreme point is identified.
Step 1. Define initial solution
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} is the extreme point, the initial arbitrary basic feasible solution can be considered as:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k \in S \quad where \; k = 0}
The letter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} denotes the number of iterations.
Step 2. Determine search direction
Search direction, that is the direction vector is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k = y_k - x_k}
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_k} are feasible extreme points and belong to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} is convex
First-order Taylor expansion around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} and problem is now reformulated to LP:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align}min \quad & z_k(y) = f(x_k) + \nabla f(x_k)^T (y-x_k) \\ s.t. \quad & y \in S \\ \end{align}}
Step 3. Determine step length
Step size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} is defined by the following formula where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} must be less than 1 to be feasible:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k + \alpha_k p_k) < f(x_k)} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle min_{\alpha \in [0,1]} \, f(x_k + \alpha p_k)}
Step 4. Set new iteration point
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1} = x_k + \alpha_k p_k}
Step 5. Stopping criterion
Check if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1}} is an approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , the extreme point. Otherwise, set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = k + 1} and return to Step 2 for the next iteration.
In the Frank-Wolfe algorithm, the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} descends after each iteration and eventually decreases towards Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} , the global minimum.
Numerical Example
Consider the non-linear problem below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} min \quad &(x-1)^2 + (y-1)^2 \\ s.t. \quad & 2x+y \leq 6 \\ & x+2y \leq 6 \\ & x \geq 0 \\ & y \geq 0 \end{align}}
ITERATION 1
Step 1. Choose a starting point
Begin by choosing the feasible point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} and take the partial derivatives of the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_x(x,y) = 2(x-1)=2x-2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_y(x,y) = 2(y-1)=2y-2 }
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \therefore \; \nabla f(0,0) = z_0 = [-2, -2] }
Step 2. Determine a search direction
Obtain the search direction by solving the linear problem that is subject to the constraints defined. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(0,0) \cdot (x,y)^T }
The solution of this linear problem is obtained via linear programming algorithm, which is the enumeration with the extreme points in the feasible region. Using the simplex method or the software GAMS, the solution to linear problem is: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(0,0) \cdot (x,y)^T = (2,2)}
Thus, the direction vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_0} for this iteration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_0 } is:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} p_0 &= (x,y)^T - z_0 \\ &= [2,2] - [-2,-2] = [4, 4] \end{align}}
Step 3. Determine step length
Evaluate Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_{\alpha_0} = f(4\alpha_0, 4\alpha_0)} to obtain step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0} .
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \because \;\; \qquad f &=(4\alpha_0-1)^2 + (4\alpha_0-1)^2 \\ &= 32\alpha_0^2 -16\alpha_0 +2 \\ \nabla f(\alpha_0) &= 64\alpha_0 - 16 = 0 \\ \therefore \qquad \alpha_0 &= 16/64 \end{align}}
Step 4. Set new iteration point
The next point is determined by the following formula:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} x_1 &= x_0 + \alpha_0p_0 \\ &= [0,0] + 16/64 \cdot [4,4] \\ \therefore \; x_1 &= [1,1] \end{align} }
Step 5. Perform optimality test
If the following equation yields a zero, the optimal solution has been found for the problem. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f_1 & = \nabla f(x_0) \cdot p_0 =\nabla f(0,0) \cdot p_0 \\ & = -2 \cdot 4 + -2 \cdot 4 = -16 \end{align}} Since the solution is not zero, the extreme point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} is not optimal and next iteration is required.
ITERATION 2
Step 1. Utilize new iteration point as the starting point
From Step 4 in Iteration 1, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1 = [1,1]} . Therefore, substituting new iteration point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1} into Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_x(x,y)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta f_y(x,y)} from Step 1, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(1,1) = z_1 = [0, 0] }
Since the gradient of the new starting point is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} , the optimality test for the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} will always yield Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_2 = \nabla f(1,1) \cdot p_1 = [0, 0] \cdot p_1}
Thus, the extreme point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,1)} is the optimum solution for this non-linear problem.
Conclusion
The Frank-Wolfe algorithm is one of the key techniques in the machine learning field. The algorithm features favor linear minimization, simple implementation, and low complexity. By using the simplex method that requires little alteration to the gradient and interpolation in each iteration, the optimization of the linearized quadratic objective function can be performed in a significantly shorter runtime and larger datasets can be processed more efficiently. Therefore, even though the convergence rate of Frank-Wolfe algorithm is slow due to the search for naive descent directions in each iteration, the benefits that the algorithm brings still outweigh the disadvantages. With the main characteristics of being projection-free and the capability of producing solutions for sparse structures, the algorithm gained popularity with many use cases in machine learning.
References
- ↑ 1.0 1.1 Frank, M. and Wolfe, P. (1956). An algorithm for quadratic programming. Naval Research Logistics Quarterly, 3(1-2):95–110.
- ↑ Combettes, C.W.. and Pokutta, S. (2020). Boosting Frank-Wolfe by chasing gradients. International Conference on Machine Learning (pp. 2111-2121). PMLR.
- ↑ Jaggi, M. (2013). Revisiting Frank-Wolfe: Projection-free sparse convex optimization. Inerational Conference on Machine Learning (pp.427-435). PMLR.