Geometric programming
Authors: Wenjun Zhu, Sam Olsen (SYSEN5800, FALL 2021)
Introduction
A geometric programming (GP) is a family of non-linear optimization problems. Geometric programming optimization problems are typically not convex optimization problems. However, geometric programming optimization problems can be transformed from non-convex optimization problems to convex optimization problems given by their special properties. The convexification for geometric programming optimization problems is implemented by a mathematical transformation of the objective function and constraint functions and a change of decision variables. Though a number of practical problems are not equivalent to geometric programming, geometric programming is generally considered an effective solution for practical problems and it is used to well approximate and analyze various large-scale applications. Typical applications include but are not limited to optimizing power control in communication systems[1], optimizing doping profile in semiconductor device engineering[2], optimizing electronic component sizing in IC design[3], and optimizing aircraft design in aerospace engineering[4].
Theory/Methodology
Monomial function
Let ... denote real positive variables,
A monomial function, or a monomial, is defined as:
= ...
where > 0, ε R
The exponents of a monomial can be any real numbers, including fractional or negative, but the coefficient can only be positive[5].
Posynomial function
Posynomial
A posynomial function, or a posynomial, is defined as: = ...
where > 0,
This is a function of sum of monomial functions[5].
Generalized Posynomial
A generalized posynomial function, or a general posynomial, is defined as a function of positive variables if it can be formed from posynomials using the operations of addition, multiplication, positive (fractional) power, and maximum[3].
For example:
where ,
,
is a generalized posynomial function and it can be seen as follows:
- is a posynomial so is a posynomial function
- is a posynomial so is a posynomial function
- and are posynomials, since it is the maximum of two posynomials, is a generalized posynomial so is a generalized posynomial function
- is expressed by addition, multiplication, and positive (fractional) power from , , functions
Therefore is a generalized posynomial function.
Definition
The standard form of Geometric Programming optimization is to minimize the objective function which must be posynomial. The inequality constraints can only have the form of a posynomial less than or equal to one, and the equality constraints can only have the form of a monomial equal to one.[3]
Standard Form
Minimize
Subject to: , = 1,...,m,
, = 1,...,p,
, = 1,...,q,
where are posynomial functions, are monomials, and are the decision variables.
Generalized Geometric Programming Form
Minimize
Subject to: , = 1,...,m,
, = 1,...,p,
where are generalized posynomial functions, are monomials, and are the decision variables.
Since any posynomial is also a generalized posynomial, any geometric programming is also generalized geometric programming.
Generalized geometric programming can be converted to equivalent geometric programming by different mathematical transformations.
Feasibility Analysis
For the generalized geometric programming problem to be feasible, the constants need to be mutually consistent.[3] where:
, = 1,...,m,
, = 1,...,p
Determining the feasibility needs to be found before optimization. If these conditions are not met, then it might be useful to find: , the closest point to feasibility. If that is the case, the following format is provided:
Minimize
Subject to: , = 1,...,m,
, = 1,...,p,
, = 1,...,m
Numerical Examples
Transform a non-standard form GP to standard form GP
The non-standard form GP is as follows:
Minimize
Subject to: ,
,
The equivalent standard form GP is as follows:
Minimize
Subject to: ,
,
,
Transform Non-convex Optimization Problems to Convex Optimization problem
The non-convex non-linear programming is as follows:
Minimize
Subject to: ,
,
The reformulation process using exponential transformation, from non-convex optimization problem to convex optimization problem, is as follows:
Let , , then the objective function becomes:
The first constraint of the problem becomes:
=>
=>
=>
The second constraint of the problem becomes:
=>
is unbounded.
The third constraint of the problem becomes:
=>
is unbounded.
Substitute the new reformulation into the original problem, the new problem becomes:
Minimize
Subject to: ,
, are unbounded.
This is a convex non-linear programming problem.
Applications
Power Control
Transmitter power control in communication system is one of the typical applications of geometric programming. The objective of the problem is to minimize the total power of the transmitters subject to transmitter power limits and the signal to interference and noise ratio (SINR) of many receiver/transmitter pairs.[1] This application demonstrates that the GP formulation allows us to handle the more general case in which the receiver interference power is any posynomial function of the powers.
Optimal Doping Profile
Doping profile in semiconductor device engineering is another typical application of geometric programming. The objective of the problem is to choose the best doping profile (also called the acceptor impurity concentration) to obtain a transistor with favorable properties. There are many factors that affect the properties of a transistor. One of the critical measures of the favorable properties of a transistor is its base transit time, which determines how fast the transistor is. Therefore, the goal is to choose the doping profile to minimize the base transit time, subject to doping profile limits, doping gradient, and initial/final doping profile values.[2]
FloorPlanning
The floor planning problem is a generalized geometric programming problem instead of a geometric programming problem. However, any generalized geometric programming problem can be mechanically transferred to any geometric programming problem. The objective of the problem is to minimize the "bounding box" area that can include all the required objects, subject to the area of the individual object and the aspect ratio of the individual object.[6]
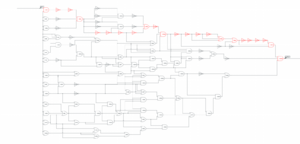
Digital Gate Sizing
The digital gate sizing problem is a generalized geometric programming problem instead of a geometric programming problem. However, any generalized geometric programming problem can be mechanically transferred to any geometric programming problem.[7] The objective of the problem is to minimize the worst-case delay of the digital signal traveling along any path through the circuit, subject to limits on the total area and power. The problem can be demonstrated as follows: To the right there is a Digital Circuit with the critical path highlighted in red. Every IC component is given power, area, resistance, and capacitance values. Using the 3 different component types: AND, OR, NOT, the total power, total area, total resistance, and total capacitance are fond for each component type. The Minimum delay, is the summation of the multiplication for each components total resistance and capacitance, with relations to bounded area and power.[8]
Conclusion
In general, geometric programming is a simple but powerful family of non-linear optimization problems. Though geometric programming optimization problems are typically not convex optimization problems, they can be transformed to convex optimization problems by multiple convexification techniques.[9] Because of convexification, geometric programming is used to solve and analyze various large-scale applications, and it is used to convert computationally intractable optimization problems to computationally tractable optimization problems.
References
- ↑ 1.0 1.1 M. Chiang, C. W. Tan, D. P. Palomar, D. O’Neill, and D. Julian,"Power Control By Geometric Programming" (JULY 2007).
- ↑ 2.0 2.1 Y.Li and Y.-C. Chen1,Optimal Channel Doping Profile of Two-Dimensional Metal-Oxide-Semiconductor Field-Effect Transistors via Geometric Programming (2015).
- ↑ 3.0 3.1 3.2 3.3 S. Boyd, S. J. Kim, L. Vandenberghe, and A. Hassibi."A Tutorial on Geometric Programming." Retrieved 20 October 2019.
- ↑ W. Hoburg and P. Abbeel. Geometric programming for aircraft design optimization. AIAA Journal 52.11 (2014): 2414-2426.
- ↑ 5.0 5.1 S. Boyd, L. Vandenberghe, Convex Optimization. Cambridge University Press, 2009.
- ↑ B. Nadhindla, H. Kakarlai, V. Gunjan, M .Reddy, Dr. F. Shaik, Geometric Programming-Based Automation of Floorplanning in ASIC Physical Design: Proceedings of the International Conference on Communications and Cyber Physical Engineering 2018. 10.1007/978-981-13-0212-1_48..
- ↑ S. -P. Boyd, S.-J. Kim, D. -D. Patil, M. -A. Horowitz,"Digital Circuit Optimization via Geometric Programming. Operations Research" (2005) 53(6):899-932.
- ↑ V. -K. Vassilev, J. -F. Miller, "Scalability Problems of Digital Circuit Evolution Evolvability and Efficient Designs", (2000) 2-10.
- ↑ Z. Perez-Rivera, E. Tlelo-Cuautle and V. Champac, Gate Sizing Methodology with a Novel Accurate Metric to Improve Circuit Timing Performance under Process Variations, (2020) 1-15..




























































