Lagrangean duality
Authors: Mariet Kurtz, Jerome Terrell, Sonam Tharkay, Ashley Turke, Daniel Yeung (SYSEN5800 Fall 2021)
Introduction
Lagrangean duality is a specific form of a broader concept known as Duality. The theory of duality originated as part of an intellectual debate and observation amongst mathematicians and colleagues John von Neumann and George Dantzig. During World War II, a discussion occurred where Dantzig shared his theory on Linear Programming and his simplex method. Von Neumann quickly surmised that Dantzig's Linear Programming shared an equivalence with his Game Theory and Expanding Economy model. Von Neumann then conceptualized the theory of using an alternate perspective, referred to as the dual problem, so that either the primal or dual problem could be solved to yield an optimal solution. In 1947, von Neumann formally published his theory of Duality. This principle would then see several formulations and implementations such as Fenchel, Wolfe, and Lagrangean.[1]
The Lagrangean dual has become a common approach to solving optimization problems. Many problems can be efficiently solved by constructing the Lagrangean function of the problem and solving the dual problem instead of the primal problem. Optimization problems can be reformulated by taking the Lagrangean and its corresponding gradient to find the optimal value of the optimization problem’s variables. These values are then substituted back into the Lagrangean and the dual problem is constructed by reformulating the optimization problem in terms of a different set of variables (dual variables).
Even when a dual problem cannot be proven to have the same optimal solution as the primal problem, Lagrangean relaxation still provides benefits. This is when an approximation can be determined by using Lagrangean multipliers to add a penalty to constraint violations. The advantage of performing Lagrangean relaxation is that in many situations it is easier to solve the dual than the primal problem.[2] For example, non-convex problems are generally more difficult to solve than convex problems. By reformulating the primal optimization problem into the Lagrangean dual problem, a difficult non-convex problem can oftentimes be turned into an easier convex problem.[3]
Algorithm
Generalization of a typical optimization problem:
Optimization Problem (in Standard Form):
The Lagrangean for the optimization problem above takes the form:
where and are the Lagrange Multipliers (dual variables).[4]
Let the dual variables be non-negative to ensure strong duality.
The Gradient of the Lagrangean is set equal to zero, to find the optimal values of ().
The Lagrangean dual function () equals the Lagrangean with values substituted out.
The Lagrangean dual optimization problem can be formulated using the following Lagrangean dual function:
At the optimal values of variables , there exist scalar Lagrangean multiplier values where the gradient of the Lagrangean is zero[5]. Hence, solving the dual problem, which is a function of the Lagrangean multipliers () yields the same solution as the primal problem, which is a function of the original variables (). For the dual solution and the primal solutions to be equal the condition has to be a strong duality. The Lagrangean takes all of the constraints and combines it with the objective function into one larger formula.
Weak and Strong Duality
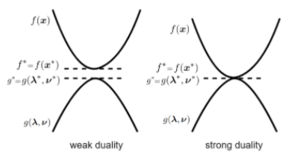
Strong duality is a concept in mathematical optimization that states the primal optimal objective and the dual optimal objective value are equal under certain conditions. Whereas, in the weak duality, the optimal value from the primal objective is greater than or equal to the dual objective. Thus, in the weak duality, the duality gap is greater than or equal to zero[7].
The verification of gaps is a convenient tool to check the optimality of solutions. As shown in the illustration, left, weak duality creates an optimality gap, while strong duality does not. Thus, the strong duality only holds true if the duality gap is equal to 0.
Complementary Slackness
From the strong duality, if both the primal optimal objective and the dual optimal objective are equal then the equation follows.[3]
is the primal optimal and the are the dual optimal. The equation shows that the duality gap is
Inf or infimum is the greatest element of a subset of a particular set is small or equal to all the elements of subset.
As seen in the process section this is the definition of dual function
The inequality shows the minimizes over . It is possible to have other minimizers however in this instance is the minimizer. This inequality follows as the Lagrangean infimum over is less than or equal to .
The last inequality shows that thus,
One important takeaway is that
Thus,
This is known as complementary slackness.
And the Complementary Slackness Conditions are:
or,
Complementary Slackness implies a relationship between the slackness in primal constraints and the slackness on the dual variable. The Complementary Slackness Theorem can be used to develop a test of optimality for a solution. Slack in corresponding inequalities must be complementary in the sense that it cannot occur simultaneously in both of them. Thus, if the primal is unbounded then the dual is infeasible and vice versa[8]. Complementary slackness is also used as a tool to find the optimal dual solution when only the optimal primal solution is known[9].
Process
Constructing the Lagrangean dual can be done in four easy steps:
Step 1: Construct the Lagrangean. The dual variables are non-negative to ensure strong duality.
Step 2: Take the partial derivatives (gradient) of the Lagrangean with respect to , set each equal to zero, and solve for .
Step 3: Substitute terms into the Lagrangean to create the dual function (), which is only a function of the dual variables ().
Step 4: Construct the dual with the dual function () and the new constraints. The dual variables are non-negative.
Numerical Example
In this section, we will apply the process to solve an example problem.
Construct the Lagrangean dual for the following optimization problem:
Step 1: Construct the Lagrangean.
Let the dual variables be non-negative to ensure strong duality.
Step 2: Take the partial derivatives of the Lagrangean with respect to , set each equal to zero, and solve for .
Step 3: Substitute terms into the Lagrangean to create the dual function (), which is only a function of the dual variables ().
Simplifies to:
Step 4: Construct the dual with the dual function () and the new constraints. The dual variables are non-negative.
Applications
The optimal solution to a dual problem is a vector of Karush-Kuhn-Tucker (KKT) multipliers (also known as Lagrange Multipliers or Dual Multipliers), thus the multipliers can be used for nonlinear programming problems to ensure the solution is indeed optimal. Since the Lagrange Multipliers can be used to ensure the optimal solution, Lagrangean duals can be applied to achieve many practical outcomes in optimization, such as determining the lower bounds for non-convex problems, simplifying the solutions of some convex problems meeting the conditions for strong duality, and determining the feasibility of a system of equations or inequalities[4]. The Lagrangean dual is used to compute the Support Vector Classifier (SVC) and effectively provides a lower bound on the objective function, which helps to characterize its solution.[10]
One application where the Lagrangean dual may be applied to find bounds for a complex problem is the symmetric Traveling Salesman Problem. This problem is analytically difficult, but its Lagrangean dual is a convex problem whose optimal solution provides a lower bound on solutions to the primal problem. While the solution to the dual problem may not be feasible in the primal problem, it is possible to use heuristic methods to find a primal solution based on the optimal dual solution[11].
Lagrangean duals have also proven useful in deep learning problems where the objective is to learn optimization problems constrained by hard physical laws. By incorporating duality during the training cycle, researchers can achieve improved results on a variety of problems, including optimizing power flows; optimizing gas compressor usage in natural gas pipelines; transprecision computing, in which the bit width of variables may be reduced to reduce power usage in embedded systems at the cost of increased error; and devising classifiers which are “fair” with respect to a defined protected characteristic[12].
The convex relaxation provided by the Lagrangean dual is also useful in the domains of machine learning[13]; combinatorial optimization, where it generalizes two well-known relaxation techniques in the field, max-stable and max-cut[14]; and 3D registration of geometric data in computer vision, where primal techniques often fail to escape local optima[15]. Lagrangean relaxation is a standard and efficient way to determine the optimal solution of NP-hard combinatorial problems.[16]
In some real-world applications, the dual formulation of a problem has a specific real-world meaning. The following are examples of real-world applications for Lagrangean Duality:
- In an electrical network, if the primal problem describes current flows, the dual problem describes voltage differences.[17]
- In an economic model, if the primal problem describes production and consumption levels, the dual problem describes the prices of goods and services.[17]
- In a structural design model, if the primal problem describes the tension of various beams, the dual problem describes nodal displacements.[17]
- In a resource allocation model, if the primal problem describes supply as seen by the production manager, the dual problem describes the demand as seen by the supplier. Applying the duality theorem towards both linear programming problems, the production levels and the prices can be set to establish a balance and equilibrium.[17]
Conclusion
Overall, Lagrangean duality is a very useful way to solve complex optimization problems, since it is often an effective strategy for reducing the difficulty of finding the solution to the original problem. The process to find the Lagrangean dual is simple and can be implemented in a wide range of problems. Lagrangean duality is used in a variety of applications, including the traveling salesman problem, deep learning models, and computer vision.
References
- ↑ A Bachem, Marting Grötschel, B H Korte, Mathematical Programming: The State of the Art. Springer-Verlag, 1983
- ↑ Claude Lemaréchal, Computational combinatorial optimization: Lagrangian Relaxation, Springer-Verlag, 2001
- ↑ 3.0 3.1 S. Boyd, L. Vandenberghe, Convex Optimization, Cambridge University Press, 2009
- ↑ 4.0 4.1 S. Wolf, S. M. Günther, An Introduction to Duality in Convex Optimization, Technische Universität München, 2011
- ↑ J. Nocedal, S. J. Wright, Numerical Optimization. Springer, 1999
- ↑ B. Ghojogh, A. Ghodsi, F. Karray, M. Crowley, KKT Conditions, First-Order and Second-Order Optimization, and Distributed Optimization: Tutorial and Survey, University of Waterloo
- ↑ R.J. Vanderbei, Linear Programming: Foundations and Extensions. Springer, 2008, http://link.springer.com/book/10.1007/978-0-387-74388-2
- ↑ J. Birge, F. Louveaux, Introduction to Stochastic Programming, Springer, 2011
- ↑ R.J. Vanderbei, Linear Programming: Foundations and Extensions. Springer, 2008
- ↑ T. Hastie, R. Tibshirani, J. Friedman. The Elements of Statistical Learning, Springer, 2009
- ↑ S. Timsj, An Application of Lagrangian Relaxation to the Traveling Salesman Problem
- ↑ F. Fioretto, P. Van Hentenryck, T. W. K. Mak, C. Tran, F. Baldo, M. Lombardi, Lagrangian Duality for Constrained Deep Learning
- ↑ J. Hui, Machine Learning - Lagrange multiplier & Dual decomposition
- ↑ C. Lemarechal, F. Oustry, Semidefinite Relaxations and Lagrangian Duality with Application to Combinatorial Optimization
- ↑ J. Briales, J. Gonzalez-Jimenez, Convex Global 3D Registration with Lagrangian Duality
- ↑ A. Ben-Tal, L.E. Ghaoui, A. Nemirovski. Robust optimization. Princeton University Press, 2009
- ↑ 17.0 17.1 17.2 17.3 R. M. Freund, Applied Lagrange Duality for Constrained Optimization, Massachusetts Institute of Technology, 2004



















































