Piecewise linear approximation
Authors: Tianhong Tan, Shoudong Zhu (CHEME 6800, 2021 Fall)
Introduction
Approximating a sophisticated non-linear function is a quite common task in industry. The very popular piecewise linear approximation can be used in a number of real-world applications such as signal processing and image processing in the electronics information sector, and pattern recognition in the AI field[1]. The piecewise linear approximation problems may be categorized into different types based on whether the segment length is fixed or not, whether the approximation is continuous or discontinuous and the norms used in the approximation process, etc.[2] By adding more nodes or segments, we may utilize the piecewise linear approximation method to represent any non-linear or linear function by any accuracy order[3]. The availability of piecewise linear approximation means that we may reduce non-linear problems into linear formations that are easier to be dealt with by machine. And of course, the expense of the corresponding algorithms would decrease a lot[4].
Theory, Methodology & Algorithms
Basics
For a function in a finite range , one can find sampling points to evaluate the function values. Then the can be approximated by a series of linear segments , where . Any given value between and can be written as the following form:
(1)
is a unique number between and .
The approximation of is calculated by a convex combination of and :
(2)
Algorithm Implementation
Though the piecewise linear approximation is quite straightforward from intuition, it is still necessary to translate the ideas discussed in the above section into some expressions that is easy for the applications in a MILP solver to deal with more complex problems. Therefore, the formulation is further developed to include both binary and continuous variables with several constraints. Then the given values are 'pushed' to become associated with the neighboring pair of consecutive break points. The constraints are listed below:
(3)
(4)
(5)
(6)
(7)
's are binary variables while 's are continuous variables from to . (3) indicates that only one takes the value of and all the other 's are . Therefore, (4) imposes that the only two 's that are non-zero are and , which are corresponding to the two neighbors of : and . (5) and (6) ensure that and , which is consistent with the expression of the approximation in (2). Finally, (7) Computes , which is the linear approximation of [5] The above formulation utilizes the idea of Special Ordered Sets (SOSs), which are powerful tools to model piecewise linear approximation problems [6]. They are defined as ordered sets of variables. In type 1 SOS (S1), only one variable can be non-zero, and 's in (3) form an S1. In type 2 SOS (S2), only two neighboring variables can be non-zero, and 's in (4) form an S2.
More Advanced Developments
To increase the accuracy of the approximation, the simplest way is just to add more nodes. Indeed, this approach can make the approximation sufficiently close to the original function as the the number of sampling points becomes large enough. However, it can be very computationally expensive. Therefore, a question has been posed: given a fixed number of segmentation lines , () and known sampling points , (), how to find a set which denotes the sampling points to be chosen as the end points of the segmentation lines so that the total squared error is minimized. To solve this optimization problem, a dynamic programming framework has been proposed. is defined as the minimum cost to the sampling points with segments. And is the minimum squared error of approximating with one segment. Then the recurrent relation can be written as: . With boundary conditions: ,, (for ), , the problem can be solved, and [7].
Numerical Example
Sampling Points Setting
In this section we consider the trigonometric function , which is widely used in engineering and many other fields, as an example. 9 evenly distributed sampling points is added for the convenience of illustration. And from the following figure, we can see that the approximation straight lines are already close enough to the original sine function just with a small number of sampling points.
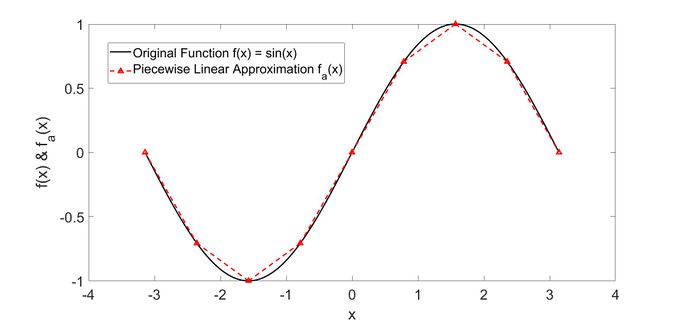
In this example, the piecewise linear approximation of for points , which correspond to , could be computed with the following constraints:
(8)
(9)
(10)
(11)
(12)
Function Value Evaluation
To compute with the above setting, the first thing to do is to determine the two non-zeros 's. In this case, they are and because is between and . Then and can be obtained by solving (10) and (11). Finally, is calculated by (12): , which is basically just a simple interpolation within the range . And it is very close to the exact value: .
It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example.
Applications
Human Computer Interface (HCI) System
Electrooculogram-based human-computer interfaces based on bio-signals are being developed in order to estimate and forecast the position of the eyeball. The large scale data provided by the signaling system, such as the eyeball's movement time and position, makes it very difficult to process. The complexity of the processing is lowered when piecewise linear approximation is introduced to the modified sliding window techniques. As a result, the system is able to capture the position of the eyeball in less than 0.2 second[8].
Wearable Sensors
To minimize the amount and dimension of data, piecewise linear approximation methods can be used to orientation sensor inputs. It indicates that data may be stored, communicated, and processed with less storage, transmission, and processing space. As a result, wearable sensors will consume less energy while collecting varied settings while maintaining broad trajectory information[9].
Artificial neural network with nonlinear activation function
Taylor series expansion, polynomial approximation, look-up table, and piecewise linear approximation can all be used to complete sigmoidal approximation in an artificial neural network. Among these methods, the approach of piecewise linear approximation is very straightforward of approximating sigmoidal functions. Because all nonlinear terms may be calculated by combining multiple straight lines with varying gradients. And then they can directly map the inputs to sigmoidal outputs. As a consequence, it produces a highly rapid approximation and a wiser method of reducing the complexity of non-linear terms[10].
Chemical Plant Planning Optimization
Plant-wide optimization of the Polyvinyl Chloride production process is demonstrated to be a mixed integer nonlinear programming problem (MINLP). This extremely complex system has a large number of nonlinear variables, such as total plant energy consumption. Because the mixed-integer linear program method is far more mature and efficient than the MINLP algorithm, a mathematical model based on piecewise approximation is presented to approximate the original MINLP model's nonlinear components. The original MINLP can be turned into a MILP model through such a transformation[11].
Conclusion
To conclude, this page provides some fundamental definitions and interpretations of piecewise linear approximation. We discussed the algorithm derivation, implementation as well as a numerical example which illustrates how to apply this technique to evaluate a non-linear function. Finally, we reviewed the applications of the piecewise linear approximation method in human computer interface systems, wearable sensors, artificial neural networks and chemical plant planning and optimization.
In a world full of nonlinear things, people are always willing to learn how to tackle the difficult nonlinearity. Fortunately, piecewise linear approximation has played an important role in the field of deterministic global optimization, significantly reducing the complexity of nonlinear items and making its simplicity vital for engineers.
References
- ↑ Manis, G., Papakonstantinou, G., Tsanakas, P.(1997).Optimal piecewise linear approximation of digitized curves, Proceedings of 13th International Conference on Digital Signal Processing, 1079-1081. https://ieeexplore.ieee.org/document/628552
- ↑ Dunham, J. G. (1986). Optimum Uniform Piecewise Linear Approximation of Planar Curves. IEEE Transactions on Pattern Analysis and Machine Intelligence, 67-75. https://ieeexplore.ieee.org/document/4767753
- ↑ Imamoto, A., Tang, B. (2008). Optimal Piecewise Linear Approximation of Convex Functions. Proceedings of the World Congress on Engineering and Computer Science. http://www.iaeng.org/publication/WCECS2008/WCECS2008_pp1191-1194.pdf
- ↑ Bradley, Hax, Magnanti.(1977). Applied Mathematical Programming, http://web.mit.edu/15.053/www/AppliedMathematicalProgramming.pdf
- ↑ D'Ambrosio, C., Lodi, A., Martello, S. (2010). Piecewise Linear Approximation of Functions of Two Varibles in MILP Models, Operations Research Letters, 38, 39-46. https://www.sciencedirect.com/science/article/abs/pii/S0167637709001072
- ↑ Tomlin, J. A. Special Ordered Sets and an Application to Gas Supply Operations Planning, Ketron Management Science, Inc., Mountain View, CA 94040-1266, USA. https://link.springer.com/article/10.1007/BF01589393
- ↑ Camponogara, E., Nazari, L. (2015) Models and Algorithms for Optimal Piecewise-Linear Function Approximation, Mathematical Problems in Engineering, 2015, Article ID 876862. http://dx.doi.org/10.1155/2015/876862
- ↑ Yang, J. J., Gang, G. W., Kim, T. S. (2018). Development of EOG-Based Human Computer Interface (HCI) System Using Piecewise Linear Approximation (PLA) and Support Vector Regression (SVR). Electronics, 7, 38. https://doi.org/10.3390/electronics7030038
- ↑ Grützmacher, F., Kempfle, J., Van Laerhoven, K., Haubelt, C. (2021). FastSW: Efficient Piecewise Linear Approximation of Quaternion-Based Orientation Sensor Signals for Motion Capturing with Wearable IMUs. Sensors, 21, 5180. https://doi.org/10.3390/s21155180
- ↑ Mishra, A., Zaheeruddin., Raj, K. (2007). Implementation of a digital neuron with nonlinear activation function using piecewise linear approximation technique, Internatonal Conference on Microelectronics, 69-72. http://10.1109/ICM.2007.4497664
- ↑ Gao, X. Y., Feng, Z. H., Wang, Y. H., Huang, X. L., Huang, D. X., Chen, T., Lian, X. (2018). Piecewise Linear Approximation Based MILP Method for PVC Plant Planning Optimization. Industrial & Engineering Chemistry Research, 57 (4), 1233-1244. https://doi.org/10.1021/acs.iecr.7b02130

![{\displaystyle [x_{1},x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d394fb72952d482a5005da3b6484d5858d5240af)


![{\displaystyle [(x_{i},f(x_{i})),(x_{i+1},f(x_{i+1}))]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f276b53aa7bc9744cb27616f702fa81d6bf04f2)













































![{\displaystyle x=[-\pi ,-0.75\pi ,-0.5\pi ,-0.25\pi ,0,0.25\pi ,0.5\pi ,0.75\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37df314aaee5d6cc65795e35b025f7fb65f96bb1)
![{\displaystyle f(x)=[0,-{\frac {\sqrt {2}}{2}},-1,-{\frac {\sqrt {2}}{2}},0,{\frac {\sqrt {2}}{2}},1,{\frac {\sqrt {2}}{2}},0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cc2847103f049825c7d9185b15586d3c038bf0d)















![{\displaystyle [x_{5},x_{6}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe7a09099fccb4dbcac4251a53b48227249ce0f)
