Piecewise linear approximation: Difference between revisions
No edit summary |
No edit summary |
||
| Line 53: | Line 53: | ||
===Function Value Evaluation=== | ===Function Value Evaluation=== | ||
To compute <math>sin(0.5)</math> under the above setting, the first thing to do is to determine the two non-zeros <math>\alpha</math>'s. In this case, they are <math>\alpha_{5}</math> and <math>\alpha_{6}</math> because <math>x'=0.5</math> is between <math>x_{5}=0</math> and <math>x_{6}=0.25\pi</math>. Then <math>\alpha_{5}</math> and <math>\alpha_{6}</math> can be obtained by solving (11) | To compute <math>sin(0.5)</math> under the above setting, the first thing to do is to determine the two non-zeros <math>\alpha</math>'s. In this case, they are <math>\alpha_{5}</math> and <math>\alpha_{6}</math> because <math>x'=0.5</math> is between <math>x_{5}=0</math> and <math>x_{6}=0.25\pi</math>. Then <math>\alpha_{5}=0.3634</math> and <math>\alpha_{6}=0.6366</math> can be obtained by solving (10) and (11). Finally, <math>f_{a}(0.5)</math> is calculated by (12): <math>f_{a}=\sum_{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times0+0.6366\times\frac{\sqrt{2}}{2}=0.4501</math>. And the exact value of <math>f(0.5)=sin(0.5)=0.4794</math>. | ||
It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example. | It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example. | ||
Revision as of 12:21, 25 November 2021
Authors: Tianhong Tan, Shoudong Zhu (CHEME 6800, 2021 Fall)
Introduction
Currently, approximating a complex non-linear function or smooth curve is very common in industry area. Like the very popular one, piecewise linear approximation, which is applied in a variety of real-world areas, such as signal processing and image processing in electronics information industry, pattern recognition in AI area[1]. The problem of piecewise linear approximation can be classified by which type of norms applied in approximating process, whether the length of segments is fixed or not and whether the approximation is continuity or discontinuity[2]. We can use piecewise linear approximation to represent any non-linear or linear function by any accuracy order by any accuracy by adding more nodes or segments until the accuracy is met[3]. The meaning of piecewise linear approximation's existence is it allow us to transform non-linear problem to be solved by linear formation, which is easier to be executed by machine and the amount of calculation is acceptable[4].
Theory, Methodology & Algorithms
Basics
For a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} in a finite range Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [x_{1}, x_{n}]} , one can find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} sampling points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{1}, x_{2}, ..., x_{n}} to evaluate the function values. Then the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} can be approximated by a series of linear segments Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [(x_{i}, f(x_{i})), (x_{i+1}, f(x_{i+1}))]} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = 1, 2, ..., n-1} . Any given value Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i+1}} can be written as the following form:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'= \lambda x_{i}+(1-\lambda )x_{i+1}} (1)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda } is a unique number between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} .
The approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x')} is calculated by a convex combination of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_{i})} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_{i+1})} :
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}(x')=\lambda f(x_{i})+(1-\lambda )f(x_{i+1})} (2)
Algorithm Implementation
Though the piecewise linear approximation is quite straightforward from intuition, it is still necessary to translate the ideas discussed in the above section into some expressions that is easy for the applications in a MILP solver to deal with more complex problems. Therefore, the formulation is further developed to include both binary and continuous variables with several constraints to force the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} values become associated with the neighboring pair of consecutive break points. The constraints are listed below:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{n}h_{i}=1} (3)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i}\leq h_{i-1}+h_{i}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i=1,2,...,n)} (4)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^{n}\alpha_{i}=1} (5)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \sum_{i=1}^{n}\alpha _{i}x_{i}} (6)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}=\sum_{i=1}^{n}\alpha _{i}f(x_{i})} (7)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} 's are binary variables while Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} 's are continuous variables from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} . (3) indicates that only one Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} takes the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1} and all the other Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} 's are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} . Therefore, (4) imposes that the only two Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} 's which are not Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0} are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i+1}} , which are corresponding to the two neighbors of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'} : Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{i+1}} . (5) and (6) ensure that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i}=\lambda} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i+1}=1 - \lambda} , which is consistent with the expression of the approximation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}} in (2). Finally, (7) Computes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}(x')} , which is the linear approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x')} [5].
The above formulation utilizes the idea of Special Ordered Sets (SOSs), which are powerful tools to model piecewise linear approximation problems [6]. They are defined as ordered sets of variables. In type 1 SOS (S1), only one variable can be non-zero, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} 's in (3) form an S1. In type 2 SOS (S2), only two neighboring variables can be non-zero, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } 's in (4) form an S2.
More Advanced Development
Numerical Example
Sampling Points Setting
Consider the trigonometric function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=sin(x), -\pi \leq x\leq \pi } , as an example. The approximation straight lines are very close to the original function with only 9 sampling points.
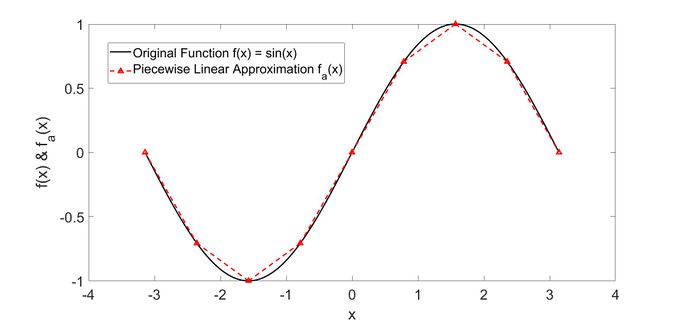
In this example, the piecewise linear approximation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = sin(x)} for points Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x= [-\pi, -0.75\pi, -0.5\pi, -0.25\pi, 0, 0.25\pi,0.5\pi,0.75\pi,\pi]} , which correspond to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=[0,-\frac{\sqrt{2}}{2},-1,-\frac{\sqrt{2}}{2},0,\frac{\sqrt{2}}{2},1,\frac{\sqrt{2}}{2},0]} , could be computed with the following constraints:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=0}^{9}h_{i}=1} (8)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _{i}\leq h_{i-1}+h_{i}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (i=1,2,...,9)} (9)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^{9}\alpha_{i}=1} (10)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x = \sum_{i=1}^{9}\alpha _{i}x_{i}} (11)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}=\sum_{i=1}^{9}\alpha _{i}sin(x_{i})} (12)
Function Value Evaluation
To compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle sin(0.5)} under the above setting, the first thing to do is to determine the two non-zeros Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} 's. In this case, they are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{5}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{6}} because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x'=0.5} is between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{5}=0} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{6}=0.25\pi} . Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{5}=0.3634} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_{6}=0.6366} can be obtained by solving (10) and (11). Finally, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}(0.5)} is calculated by (12): Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_{a}=\sum_{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times0+0.6366\times\frac{\sqrt{2}}{2}=0.4501} . And the exact value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(0.5)=sin(0.5)=0.4794} .
It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example.
Applications
Conclusion
References
- ↑ G. Manis, G. Papakonstantinou and P. Tsanakas, "Optimal piecewise linear approximation of digitized curves," Proceedings of 13th International Conference on Digital Signal Processing, 1997, pp. 1079-1081 vol.2, doi: 10.1109/ICDSP.1997.628552.
- ↑ J. G. Dunham, "Optimum Uniform Piecewise Linear Approximation of Planar Curves," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-8, no. 1, pp. 67-75, Jan. 1986, doi: 10.1109/TPAMI.1986.4767753.
- ↑ Optimal Piecewise Linear Approximation of Convex Functions A. Imamoto, B. Tang, Member, IAENG, Proceedings of the World Congress on Engineering and Computer Science 2008 WCECS 2008, October 22 - 24, 2008, San Francisco, USA.
- ↑ Applied Mathematical Programming by Bradley, Hax, and Magnanti (Addison Wesley,1977) http://web.mit.edu/15.053/www/AppliedMathematicalProgramming.pdf
- ↑ D'Ambrosio, C., Lodi, A., Martello, S. (2010). Piecewise Linear Approximation of Functions of Two Varibles in MILP Models, Operations Research Letters, 38, 39-46.
- ↑ Tomlin, J. A., “Special Ordered Sets and an Application to Gas Supply Operations Planning”, Ketron Management Science, Inc., Mountain View, CA 94040-1266, USA.