Piecewise linear approximation: Difference between revisions

Revision as of 12:41, 25 November 2021

Authors: Tianhong Tan, Shoudong Zhu (CHEME 6800, 2021 Fall)

Introduction

Currently, approximating a complex non-linear function or smooth curve is very common in industry area. Like the very popular one, piecewise linear approximation, which is applied in a variety of real-world areas, such as signal processing and image processing in electronics information industry, pattern recognition in AI area^[1]. The problem of piecewise linear approximation can be classified by which type of norms applied in approximating process, whether the length of segments is fixed or not and whether the approximation is continuity or discontinuity^[2]. We can use piecewise linear approximation to represent any non-linear or linear function by any accuracy order by any accuracy by adding more nodes or segments until the accuracy is met^[3]. The meaning of piecewise linear approximation's existence is it allow us to transform non-linear problem to be solved by linear formation, which is easier to be executed by machine and the amount of calculation is acceptable^[4].

Theory, Methodology & Algorithms

Basics

For a function $f(x)$ in a finite range $[x_{1},x_{n}]$ , one can find $n$ sampling points $x_{1},x_{2},...,x_{n}$ to evaluate the function values. Then the $f(x)$ can be approximated by a series of linear segments $[(x_{i},f(x_{i})),(x_{i+1},f(x_{i+1}))]$ , where $i=1,2,...,n-1$ . Any given value $x'$ between $x_{i}$ and $x_{i+1}$ can be written as the following form:

$x'=\lambda x_{i}+(1-\lambda )x_{i+1}$ (1)

$\lambda$ is a unique number between $0$ and $1$ .

The approximation of $f(x')$ is calculated by a convex combination of $f(x_{i})$ and $f(x_{i+1})$ :

$f_{a}(x')=\lambda f(x_{i})+(1-\lambda )f(x_{i+1})$ (2)

Algorithm Implementation

Though the piecewise linear approximation is quite straightforward from intuition, it is still necessary to translate the ideas discussed in the above section into some expressions that is easy for the applications in a MILP solver to deal with more complex problems. Therefore, the formulation is further developed to include both binary and continuous variables with several constraints to force the $x'$ values become associated with the neighboring pair of consecutive break points. The constraints are listed below:

$\sum _{i=0}^{n}h_{i}=1$ (3)

$\alpha _{i}\leq h_{i-1}+h_{i}$ $(i=1,2,...,n)$ (4)

$\sum _{i=1}^{n}\alpha _{i}=1$ (5)

$x=\sum _{i=1}^{n}\alpha _{i}x_{i}$ (6)

$f_{a}=\sum _{i=1}^{n}\alpha _{i}f(x_{i})$ (7)

$h$ 's are binary variables while $\alpha$ 's are continuous variables from $0$ to $1$ . (3) indicates that only one $h$ takes the value of $1$ and all the other $h$ 's are $0$ . Therefore, (4) imposes that the only two $\alpha$ 's which are not $0$ are $\alpha _{i}$ and $\alpha _{i+1}$ , which are corresponding to the two neighbors of $x'$ : $x_{i}$ and $x_{i+1}$ . (5) and (6) ensure that $\alpha _{i}=\lambda$ and $\alpha _{i+1}=1-\lambda$ , which is consistent with the expression of the approximation $f_{a}$ in (2). Finally, (7) Computes $f_{a}(x')$ , which is the linear approximation of $f(x')$ ^[5].

The above formulation utilizes the idea of Special Ordered Sets (SOSs), which are powerful tools to model piecewise linear approximation problems ^[6]. They are defined as ordered sets of variables. In type 1 SOS (S1), only one variable can be non-zero, and $h$ 's in (3) form an S1. In type 2 SOS (S2), only two neighboring variables can be non-zero, and $\alpha$ 's in (4) form an S2.

A more Advanced Development

Numerical Example

Sampling Points Setting

In this section we consider the trigonometric function $f(x)=sin(x),-\pi \leq x\leq \pi$ , which is widely used in engineering and many other fields, as an example. 9 evenly distributed sampling points is added for the convenience of illustration. And from the following figure, we can see that the approximation straight lines are already close enough to the original sine function just with a small number of sampling points.

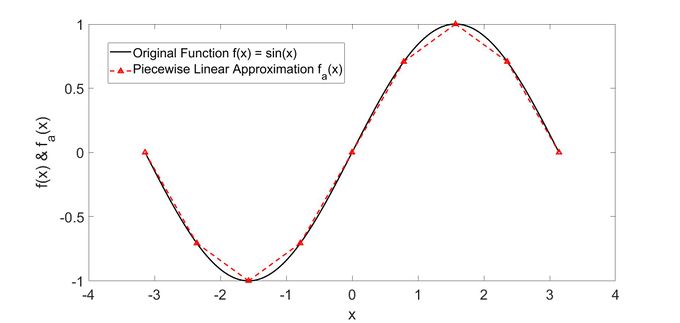
In this example, the piecewise linear approximation of $f(x)=sin(x)$ for points $x=[-\pi ,-0.75\pi ,-0.5\pi ,-0.25\pi ,0,0.25\pi ,0.5\pi ,0.75\pi ,\pi ]$ , which correspond to $f(x)=[0,-{\frac {\sqrt {2}}{2}},-1,-{\frac {\sqrt {2}}{2}},0,{\frac {\sqrt {2}}{2}},1,{\frac {\sqrt {2}}{2}},0]$ , could be computed with the following constraints:

$\sum _{i=0}^{9}h_{i}=1$ (8)

$\alpha _{i}\leq h_{i-1}+h_{i}$ $(i=1,2,...,9)$ (9)

$\sum _{i=1}^{9}\alpha _{i}=1$ (10)

$x=\sum _{i=1}^{9}\alpha _{i}x_{i}$ (11)

$f_{a}=\sum _{i=1}^{9}\alpha _{i}sin(x_{i})$ (12)

Function Value Evaluation

To compute $sin(0.5)$ with the above setting, the first thing to do is to determine the two non-zeros $\alpha$ 's. In this case, they are $\alpha _{5}$ and $\alpha _{6}$ because $x'=0.5$ is between $x_{5}=0$ and $x_{6}=0.25\pi$ . Then $\alpha _{5}=0.3634$ and $\alpha _{6}=0.6366$ can be obtained by solving (10) and (11). Finally, $f_{a}(0.5)$ is calculated by (12): $f_{a}=\sum _{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times 0+0.6366\times {\frac {\sqrt {2}}{2}}=0.4501$ , which is basically just a simple interpolation bewteen $x_{5}$ and $x_{6}$ . And it is very close to the exact value: $f(0.5)=sin(0.5)=0.4794$ .

It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example.

Applications

Conclusion

References

↑ G. Manis, G. Papakonstantinou and P. Tsanakas, "Optimal piecewise linear approximation of digitized curves," Proceedings of 13th International Conference on Digital Signal Processing, 1997, pp. 1079-1081 vol.2, doi: 10.1109/ICDSP.1997.628552.
↑ J. G. Dunham, "Optimum Uniform Piecewise Linear Approximation of Planar Curves," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-8, no. 1, pp. 67-75, Jan. 1986, doi: 10.1109/TPAMI.1986.4767753.
↑ Optimal Piecewise Linear Approximation of Convex Functions A. Imamoto, B. Tang, Member, IAENG, Proceedings of the World Congress on Engineering and Computer Science 2008 WCECS 2008, October 22 - 24, 2008, San Francisco, USA.
↑ Applied Mathematical Programming by Bradley, Hax, and Magnanti (Addison Wesley,1977) http://web.mit.edu/15.053/www/AppliedMathematicalProgramming.pdf
↑ D'Ambrosio, C., Lodi, A., Martello, S. (2010). Piecewise Linear Approximation of Functions of Two Varibles in MILP Models, Operations Research Letters, 38, 39-46.
↑ Tomlin, J. A., “Special Ordered Sets and an Application to Gas Supply Operations Planning”, Ketron Management Science, Inc., Mountain View, CA 94040-1266, USA.

[1] G. Manis, G. Papakonstantinou and P. Tsanakas, "Optimal piecewise linear approximation of digitized curves," Proceedings of 13th International Conference on Digital Signal Processing, 1997, pp. 1079-1081 vol.2, doi: 10.1109/ICDSP.1997.628552.

[2] J. G. Dunham, "Optimum Uniform Piecewise Linear Approximation of Planar Curves," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-8, no. 1, pp. 67-75, Jan. 1986, doi: 10.1109/TPAMI.1986.4767753.

[3] Optimal Piecewise Linear Approximation of Convex Functions A. Imamoto, B. Tang, Member, IAENG, Proceedings of the World Congress on Engineering and Computer Science 2008 WCECS 2008, October 22 - 24, 2008, San Francisco, USA.

[4] Applied Mathematical Programming by Bradley, Hax, and Magnanti (Addison Wesley,1977) http://web.mit.edu/15.053/www/AppliedMathematicalProgramming.pdf

[5] D'Ambrosio, C., Lodi, A., Martello, S. (2010). Piecewise Linear Approximation of Functions of Two Varibles in MILP Models, Operations Research Letters, 38, 39-46.

[6] Tomlin, J. A., “Special Ordered Sets and an Application to Gas Supply Operations Planning”, Ketron Management Science, Inc., Mountain View, CA 94040-1266, USA.

[1]

[2]

[3]

[4]

[5]

[6]

@@ Line 53: / Line 53: @@
 ===Function Value Evaluation===
-To compute <math>sin(0.5)</math> with the above setting, the first thing to do is to determine the two non-zeros <math>\alpha</math>'s. In this case, they are <math>\alpha_{5}</math> and <math>\alpha_{6}</math> because <math>x'=0.5</math> is between <math>x_{5}=0</math> and <math>x_{6}=0.25\pi</math>. Then <math>\alpha_{5}=0.3634</math> and <math>\alpha_{6}=0.6366</math> can be obtained by solving (10) and (11). Finally, <math>f_{a}(0.5)</math> is calculated by (12): <math>f_{a}=\sum_{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times0+0.6366\times\frac{\sqrt{2}}{2}=0.4501</math>. And it is very close to the exact value: <math>f(0.5)=sin(0.5)=0.4794</math>.
+To compute <math>sin(0.5)</math> with the above setting, the first thing to do is to determine the two non-zeros <math>\alpha</math>'s. In this case, they are <math>\alpha_{5}</math> and <math>\alpha_{6}</math> because <math>x'=0.5</math> is between <math>x_{5}=0</math> and <math>x_{6}=0.25\pi</math>. Then <math>\alpha_{5}=0.3634</math> and <math>\alpha_{6}=0.6366</math> can be obtained by solving (10) and (11). Finally, <math>f_{a}(0.5)</math> is calculated by (12): <math>f_{a}=\sum_{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times0+0.6366\times\frac{\sqrt{2}}{2}=0.4501</math>, which is basically just a simple interpolation bewteen <math>x_{5}</math> and <math>x_{6}</math>. And it is very close to the exact value: <math>f(0.5)=sin(0.5)=0.4794</math>.
 It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example.