Piecewise linear approximation

Authors: Tianhong Tan, Shoudong Zhu (CHEME 6800, 2021 Fall)

Introduction

Currently, approximating a complex non-linear function or smooth curve is very common in industry area. Like the very popular one, piecewise linear approximation, which is applied in a variety of real-world areas, such as signal processing and image processing in electronics information industry, pattern recognition in AI area. The problem of piecewise linear approximation can be classified by which type of norms applied in approximating process, whether the length of segments is fixed or not and whether the approximation is continuity or discontinuity. We can use piecewise linear approximation to represent any non-linear or linear function by any accuracy order by any accuracy by adding more nodes or segments until the accuracy is met. The meaning of piecewise linear approximation's existence is it allow us to transform non-linear problem to be solved by linear formation, which is easier to be executed by machine and the amount of calculation is acceptable.

Theory, Methodology & Algorithms

Basics

For a function $f(x)$ in a finite range $[x_{1},x_{n}]$, one can find $n$ sampling points $x_{1},x_{2},...,x_{n}$ to evaluate the function values. Then the $f(x)$ can be approximated by a series of linear segments $[(x_{i},f(x_{i})),(x_{i+1},f(x_{i+1}))]$, where $i=1,2,...,n-1$. Any given value $x'$ between $x_{i}$ and $x_{i+1}$ can be written as the following form:

$x'=\lambda x_{i}+(1-\lambda )x_{i+1}$ (1)

$\lambda$ is a unique number between $0$ and $1$.

The approximation of $f(x')$ is calculated by a convex combination of $f(x_{i})$ and $f(x_{i+1})$:

$f_{a}(x')=\lambda f(x_{i})+(1-\lambda )f(x_{i+1})$ (2)

Algorithm Implementation

Though the piecewise linear approximation is quite straightforward from intuition, it is still necessary to translate the ideas discussed in the above section into some expressions that is easy for the applications in a MILP solver to deal with more complex problems. Therefore, the formulation is further developed to include both binary and continuous variables with several constraints. Then the $x'$ values are 'pushed' to become associated with the neighboring pair of consecutive break points. The constraints are listed below:

$\sum _{i=0}^{n}h_{i}=1$ (3)

$\alpha _{i}\leq h_{i-1}+h_{i}$ $(i=1,2,...,n)$ (4)

$\sum _{i=1}^{n}\alpha _{i}=1$ (5)

$x=\sum _{i=1}^{n}\alpha _{i}x_{i}$ (6)

$f_{a}=\sum _{i=1}^{n}\alpha _{i}f(x_{i})$ (7)

$h$'s are binary variables while $\alpha$'s are continuous variables from $0$ to $1$. (3) indicates that only one $h$ takes the value of $1$ and all the other $h$'s are $0$. Therefore, (4) imposes that the only two $\alpha$'s that are non-zero are $\alpha _{i}$ and $\alpha _{i+1}$, which are corresponding to the two neighbors of $x'$: $x_{i}$ and $x_{i+1}$. (5) and (6) ensure that $\alpha _{i}=\lambda$ and $\alpha _{i+1}=1-\lambda$, which is consistent with the expression of the approximation $f_{a}$ in (2). Finally, (7) Computes $f_{a}(x')$, which is the linear approximation of $f(x')$.

The above formulation utilizes the idea of Special Ordered Sets (SOSs), which are powerful tools to model piecewise linear approximation problems . They are defined as ordered sets of variables. In type 1 SOS (S1), only one variable can be non-zero, and $h$'s in (3) form an S1. In type 2 SOS (S2), only two neighboring variables can be non-zero, and $\alpha$'s in (4) form an S2.

More Advanced Developments

To increase the accuracy of the approximation, the simplest way is just to add more nodes. Indeed, this approach can make the approximation sufficiently close to the original function as the the number of sampling points becomes large enough. However, it can be very computationally expensive. Therefore, a question has been posed: given a fixed number of segmentation lines $R=\left\{r_{1},r_{2},...,r_{T}\right\}$, ($r_{t}=a_{t}x+b_{t},t=1,2,...,T$) and $n$ known sampling points $P=\left\{p_{1},p_{2},...,p_{n}\right\}$, ($T<n$), how to find a set $I=\left\{i(1)=1,i(2),...,i(T+1)=n\right\}$ which denotes the sampling points to be chosen as the end points of the segmentation lines so that the total squared error $\sum _{t=1}^{T}E_{t}=\sum _{t=1}^{T}\sum _{k=i(t)}^{i(t+1)}(y_{k}-a_{t}x_{k}-b_{t})^{2}$ is minimized. To solve this optimization problem, a dynamic programming framework has been proposed. $F(j,t)$ is defined as the minimum cost to the sampling points $\left\{p_{1},p_{2},...,p_{j}\right\}$ with $t$ segments. And $E(i,j)$ is the minimum squared error of approximating $\left\{p_{i},...,p_{j}\right\}$ with one segment. Then the recurrent relation can be written as: $F(j,t)=minF(i,t-1)+E(i,j)$. With boundary conditions: $E(i,i)=\infty$ ,$F(j,t)=\infty$, (for $j\leq t$), $F(j,1)=E(j,1)$, the problem can be solved, and $F(n,t)=minE$.

Numerical Example

Sampling Points Setting

In this section we consider the trigonometric function $f(x)=sin(x),-\pi \leq x\leq \pi$, which is widely used in engineering and many other fields, as an example. 9 evenly distributed sampling points is added for the convenience of illustration. And from the following figure, we can see that the approximation straight lines are already close enough to the original sine function just with a small number of sampling points.

Fig.1 Piecewise linear approximation of f(x) = sin(x)

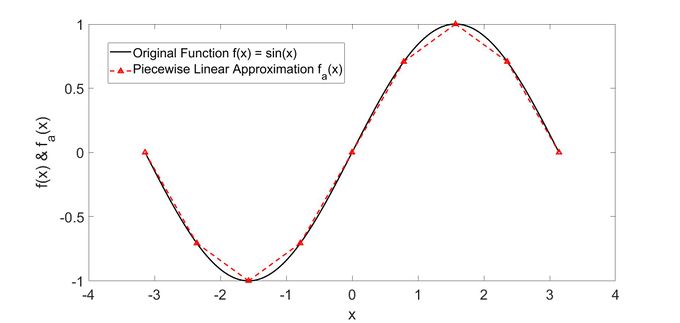
In this example, the piecewise linear approximation of $f(x)=sin(x)$ for points $x=[-\pi ,-0.75\pi ,-0.5\pi ,-0.25\pi ,0,0.25\pi ,0.5\pi ,0.75\pi ,\pi ]$, which correspond to $f(x)=[0,-{\frac {\sqrt {2}}{2}},-1,-{\frac {\sqrt {2}}{2}},0,{\frac {\sqrt {2}}{2}},1,{\frac {\sqrt {2}}{2}},0]$, could be computed with the following constraints:

$\sum _{i=0}^{9}h_{i}=1$ (8)

$\alpha _{i}\leq h_{i-1}+h_{i}$ $(i=1,2,...,9)$ (9)

$\sum _{i=1}^{9}\alpha _{i}=1$ (10)

$x=\sum _{i=1}^{9}\alpha _{i}x_{i}$ (11)

$f_{a}=\sum _{i=1}^{9}\alpha _{i}sin(x_{i})$ (12)

Function Value Evaluation

To compute $sin(0.5)$ with the above setting, the first thing to do is to determine the two non-zeros $\alpha$'s. In this case, they are $\alpha _{5}$ and $\alpha _{6}$ because $x'=0.5$ is between $x_{5}=0$ and $x_{6}=0.25\pi$. Then $\alpha _{5}=0.3634$ and $\alpha _{6}=0.6366$ can be obtained by solving (10) and (11). Finally, $f_{a}(0.5)$ is calculated by (12): $f_{a}=\sum _{i=1}^{9}\alpha _{i}sin(x_{i})=0.3634\times 0+0.6366\times {\frac {\sqrt {2}}{2}}=0.4501$, which is basically just a simple interpolation within the range $[x_{5},x_{6}]$. And it is very close to the exact value: $f(0.5)=sin(0.5)=0.4794$.

It is worth noticing that more sampling points can be added to increase the accuracy of the approximation. And these discretization points do not necessarily to be evenly distributed as what is shown in this example.

Applications

Human Computer Interface (HCI) System

Electrooculogram based human-computer interfaces, which are designed to estimate and predict the position of eyeball are proposed based on bio-signal. However, large scale data that the signaling system produced, like the eyeball’s movement time and eyeball’s position are very hard to handle, piecewise linear approximation is added to modified sliding window algorithms in order to reduce the complexity of the process, which can capture the position of the eyeball’s position in less than 0.2 second..

Wearable Sensors

Piecewise linear approximation algorithms can be applied to orientation sensor signals in order to reduce the amount and the dimension of data, which means that the data can be stored, transmitted and processed with less space. Therefore, wearable sensors will reduce consuming the energy when they are capturing different scenarios, while at the same time it does not lose general trajectory information.

Artificial neural network with nonlinear activation function

In artificial neural network, sigmoidal approximation can be finished by Taylor series expansion, Polynomial approximation and look-up table and piecewise linear approximation. But the piecewise linear approximation method is an extremely direct way to approximate sigmoidal function, because all the calculation of nonlinear terms can be done by combining different straight lines of different gradient, which can directly map the inputs to sigmoidal outputs. In this way, it results a very fast approximation and a smarter way to reduce the complexity of non-linear terms.

Chemical Plant Planning Optimization

Plant-wide planning optimization of PVC production process is proved to be a mixed integer nonlinear programming (MINLP), where includes highly nonlinear term, like the whole plant energy consumption. As the mixed-integer linear program algorithm is much more mature and efficient than MINLP algorithm, a mathematic model based on piecewise approximation is proposed to approximate the nonlinear terms of the original MINLP model. In such transformation, the original MINLP can be transformed into a MILP model.

Conclusion

Piecewise approximation played a key role in deterministic global optimization area, which definitely reduce the complexities of nonlinear items and its simplicity is indispensable for engineers.