Portfolio optimization
Authors: Fanghan Li, Kevin Pan, Qizeng Sun, Hanshen Li, Eric Luo, SYSEN 5800 Fall 2021
Introduction
Portfolio optimization is a way to maximize net gains in a portfolio while minimizing risk. A portfolio is a set of selected stocks chosen by the investor. Risk is defined by the potential associated lost of some or all the original investment. Returns are the associated gains when the price of the stocks increases beyond the original investment. By applying probability statistics, linear algebra, optimization and other methods to redistribute the investment portfolio under the established target returns and risk limits to achieve the goal of reducing risks or obtaining higher benefits under the same risk conditions.[1]
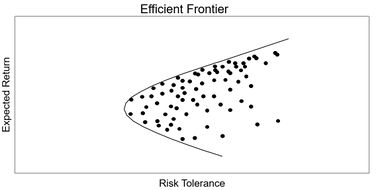
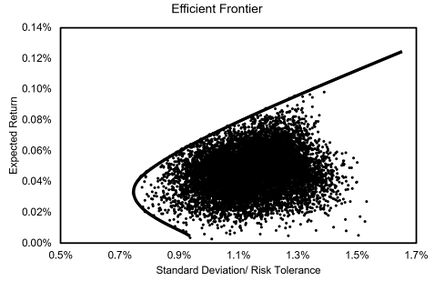
Risk is a major factor in choosing stocks in a portfolio. In order to mitigate these risks, investors typically use an efficient frontier graph as shown in figure 1.
The x- axis represents the standard deviation of the data, which is also known as the risk tolerance. On the y- axis is the expected percent return. The points near the solid line are optimal, which is also known as the frontier line. Any points that fall below the curve are considered to be nonoptimal. This is due to the fact that with the same risk tolerance there are better expected returns. This method has its limitations as it relies on past data.[2]
Theory
Modern Portfolio Theory (MPT) or mean variance analysis is a mathematical framework introduced by the economist Harry Markowitz. MPT is used to combine a portfolio of assets in order to maximize the expected return under a given level of risk. Its main point is that investors can choose the best combination of asset risk and return based on the assessment of individual risk tolerance, so as to obtain the most ideal results.[3]
The mitigation of risk can be characterized as follows. Let be a matrix of the daily returns, where is the number of stocks and is the number of days that are being analyzed.
represents the expected returns of the stock which is the average of the individual column of . is the standard deviation of the individual the data set of an individual stock, where is the variance.[4]
X represents the daily return subtracted by the expected returns of each respective stock. The variance and covariance table is a vital tool as it allows the user to estimate volatility of the overall portfolio.
This table will span the size of the number of stocks chosen .
is the expected return of the portfolio, where is the percent of the initial capital being allocated into each stock.[5]
represents the standard deviation of the portfolio.[6]
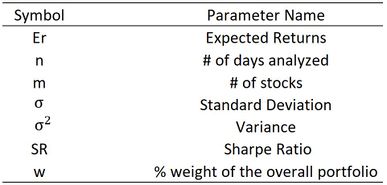
is the sharpe ratio of the portfolio. The sharpe ratio is a risk to return ratio that allows the investor to identify if the investment is worth the risk.
Methodology
Portfolio optimization could be solved and analyzed by Linear Programming and statistics. When figuring out the maximum return under the fixed risks investment projects it can be seen as follows:
| Function | Max ri*Xi |
|---|---|
| Factor: Xi | The amount of investment project i should invest |
| Coefficient: ri | The risk of investment project i |
| Constants | The limit requirements |
Table 2: Fixed Risk Table
The constraints of portfolio optimization are various, include[5]:
| Constraints | Explanation |
|---|---|
| Monetary Value Constraints | Control the amount of money in the portfolio |
| Maximum Weight Constraints | Limit the proportion of assets in the portfolio. |
| Risk Fraction Constraints | Control the number of variances that each asset may have. |
| Number of Assets Held/ Traded Constraints | Limit the number of assets held/traded in the portfolio. |
| Count Constraints | Limit the number of assets that show in each category of a category variable |
| Cost Constraints | Limit the transaction cost |
| Expected Return Constraints | Control the predicted expected return of the portfolio |
| Volatility Constraints | Constrain the predicted volatility of the portfolio(Calculate by predicted variance matrix) |
| Forced Trade Constraints | Trade with assets of at lease a certain size |
Table 3: Constraints
Several types of constraints will be selected to formulate the final return. The difference of constraints depends on the differences in investment projects, and related policy requirements, etc.[7]
Numerical Example
Example 1:
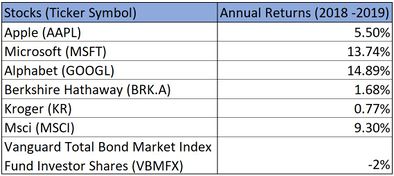
Now the investor is looking for investment opportunities for $200000, and the financial analyst identified seven investment opportunities and projected their annual rates of return. The investor is required to figure out a portfolio that could receive maximum returns.
Defining the following decision variables:
: dollars invested in AAPL
: dollars invested in MSFT
: dollars invested in GOOGL
Objective: Maximizing return
Define the constraints:
(amount invested)
The simplex table can be derived as the following:
The least coefficient is found to be row 2, where the constant is divided by . Once the pivot is found then the row reduction can begin.
There are 3 negative terms in the last row, row reduction will occur for column .
There are 2 negative terms in the last row, row reduction will occur for column .
There is now 1 negative terms in the last row, row reduction will occur for column
There is no need to conduct further calculations as all values in the last row are now positive. Therefore, the optimal solution is achieved:
(optimal solution)
Conclusion: Therefore, if the portfolio is $100,000in MSFT, $100,000 in GOOGL, $0 in AAPL,
Example 2:
Using the same 7 stocks as the first example, matrix A represents the daily closing value of each stock collected. It is a matrix the size of 7x251 where 251 is the number of available trading days in the year 2018.
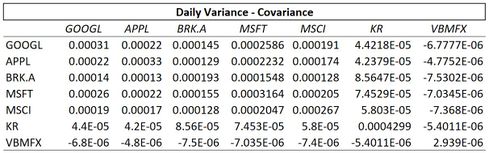
Where X is a matrix that contains the daily percent return. Er is the estimated return. With that being said the variance and covariance can then be calculated as shown.
Defining the following decision variables:
: dollars invested in AAPL
: dollars invested in MSFT
: dollars invested in GOOGL
: dollars invested in BRK.A
: dollars invested in KR
: dollars invested in MSCI
: dollars invested in VBMFX
Objective: Maximizing the SR value for optimal risk to returns ratio
With the following constraints:
(percentage needs to add up to 100)
(at least 5% weight on each stock)
Solution:
Optimal solution: Sharpe ratio = 0.05087 [unitless]
The scatter plot represents the first 10,000 random weight stocks. The optimal regions are on and near the line. It shows that larger gains come with larger risks. The graph allows the characterization of the performance of different weighted stocks in a portfolio.
Applications
Portfolio optimization is often used for investment screening and investment amount allocation. The operation of this model gives investors the opportunity to avoid risks as much as possible while obtaining the maximum relevant benefits. At the same time, after entering the constraints, the model will give reasonable investment allocation suggestions and related optimal returns. [8]
Retirement fund investment portfolio is one of the specific applications of investment portfolio optimization in modern times. Retirement planning needs to determine the source of income, estimate expenses, implement savings plans, and manage assets and risks. In the field of asset management and risk, modern financial theory advocates focusing on the total return of retirement-oriented investment portfolios rather than income. When the investment portfolio needs to be allocated, investors can choose between different asset classes and adjust their investment shares. [9]
Conclusion
Linear programming is an applicable tool in the optimization of stock portfolios. With the sharpe ratio, the tools yield returns with less risks associated as the method selects stocks and allocates investments accordingly. The optimization method will assist with new stock portfolios. It maximizes returns with the incorporation of the users risk tolerance.[10]
Reference
- ↑ Vanderbei, R. J. (2000). Linear programming: Foundations and extensions. Boston: Kluwer.
- ↑ Best, M. J. (2010). Champman & Hall/CRC Finance: Portfolio Optimization. Ontario: Canada.
- ↑ “Harry Markowitz's Modern Portfolio Theory [the Efficient Frontier].” Guided Choice, 14 Feb. 2020, https://www.guidedchoice.com/video/dr-harry-markowitz-father-of-modern-portfolio-theory/. “Constraints: Portfolio Probe: Generate
- ↑ Andre F. “Large-Scale Portfolio Optimization.” Management Science, vol. 30, no. 10, 1984, pp. 1143–1160., https://doi.org/10.1287/mnsc.30.10.1143.
- ↑ 5.0 5.1 Random Portfolios. Fund Management Software by Burns Statistics.” Portfolio Probe | Investment Technology for the 21st Century, 19 Apr. 2012, https://www.portfolioprobe.com/features/constraints/.
- ↑ Disatnik, David, and Saggi Katz. “Portfolio Optimization Using a Block Structure for the Covariance Matrix.” Journal of Business Finance & Accounting, 2012, https://doi.org/10.1111/j.1468-5957.2012.02279.x.
- ↑ Ahmed, Shabbir. Isye 6669: Deterministic Optimization ... - Isye Home | Isye. 2002, https://www2.isye.gatech.edu/~sahmed/isye6669/notes/portfolio.
- ↑ DeMiguel, Victor, et al. “A Generalized Approach to Portfolio Optimization: Improving Performance by Constraining Portfolio Norms.” Management Science, vol. 55, no. 5, 2009, pp. 798–812., https://doi.org/10.1287/mnsc.1080.0986.
- ↑ Armstrong, Frank. “How to Create a Retirement Portfolio Strategy.” Investopedia, Investopedia, 22 Aug. 2021, https://www.investopedia.com/articles/retirement/11/implement-effective-retirement-income-strategy.asp#toc-a-balanced-portfolio.
- ↑ Overton, M. L. (1997). Linear Programming












































