Trust-region methods: Difference between revisions
mNo edit summary |
|||
| (30 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Autor: Chun-Yu Chou | Autor: Chun-Yu Chou, Ting-Guang Yeh, Yun-Chung Pan, Chen-Hua Wang (CHEME 6800, Fall 2021) | ||
=Introduction= | =Introduction= | ||
Trust region method is a numerical optimization method that is employed to solve non-linear programming (NLP) problems<ref>Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization, ''Cambridge university press'', <nowiki>https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf</nowiki></ref>. Instead of finding an objective solution of the original function, the method defines a neighborhood around the current best solution as a trust region in each step (typically by using a quadratic model), which is capable of representing the function appropriately, to derive the next local optimum. Different from line search<ref>Nocedal, J., & Wright, S. (2006). Numerical optimization, ''Springer Science & Business Media'', <nowiki>https://www.math.uci.edu/~qnie/Publications/NumericalOptimization.pdf</nowiki></ref>, the model selects the direction and step size simultaneously. For example, in a minimization problem, if the decrease in the value of the optimal solution is not sufficient since the region is too large to get close to the minimizer of the objective function, the region should be shrunk to find the next best point. On the other hand, if such a decrease is significant, it is believed that the model has an adequate representation of the problem. Generally, the step direction depends on the extent that the region is altered in the previous iteration<ref>Erway, J. B., Gill, P. E., & Griffin, J. D. (2009). Iterative methods for finding a trust-region step, ''SIAM Journal on Optimization'', <nowiki>https://www.math.uci.edu/~qnie/Publications/NumericalOptimization.pdf</nowiki></ref>. | |||
=Methodology and theory= | |||
The quadratic model function <math>m_k</math> is based on derivative information at <math>x_k</math> and possibly also on information accumulated from previous iterations and steps. | |||
<math>m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^TB_kp</math> | |||
where | |||
<math>f_k=f(x_k), \bigtriangledown f_k=\bigtriangledown f(x_k)</math>, and <math>B_k</math> is symmetric matrix. | |||
Taylor’s theorem is used as a mathematical tool to study minimizers of smooth functions. | |||
<math>f(x_k + p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^T\bigtriangledown ^2f(x_k + tp)p</math> | |||
The first two terms of <math>m_k</math> are assumed to be identical to the first two terms of the Taylor-series expansion. | |||
<math>m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + O(||p^2||)</math> | |||
The difference between <math>m_k(p)</math> and <math>f (x_k + p)</math> is O. Therefore, when <math>p</math> is small, the approximation error is small. | |||
To obtain each step, we seek a solution to the subproblem as shown below. | |||
<math>\min_{p\in\R} m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^TB_kp</math> | |||
s.t <math>||p^2||\leqq\Delta _k</math> | |||
The strategies for finding approximate solutions are introduced as follows, which achieve at least as so-called Cauchy point. This point is simply the minimizer of <math>m_k</math> along the steepest descent direction that is subject to the trust region bound. | |||
'''Cauchy point calculation''' | '''Cauchy point calculation''' | ||
<math> | Similar to the line search method which does not require optimal step lengths to be convergent, the trust-region method is sufficient for global convergence purposes to find an approximate solution <math>p_k</math> that lies within the trust region. Cauchy step <math>p_k^c</math> is an inexpensive method( no matrix factorization) to solve trust-region subproblem. Furthermore, the Cauchy point has been valued because it can be globally convergent. Following is a closed-form equation of the Cauchy point. | ||
<math>p_k^c=-\tau _k\frac{\Delta k}{\left \| \bigtriangledown f_k \right \|}\bigtriangledown f_k</math> | |||
where | |||
<math>\displaystyle \tau _k={\begin{cases}1,&{\text{if }}\bigtriangledown f_k^TB_k\bigtriangledown f_k\leq 0\\min\left ( \left \| \bigtriangledown f_k \right \|^{3}/\left ( \bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k \right ),1 \right ),&{\text{otherwise }}\end{cases}}</math> | |||
Although it is inexpensive to apply the Cauchy point, the steepest descent methods sometimes perform poorly. Thus, we introduce some improving strategies. The improvement strategies is based on <math>B_k</math> where it contains valid curvature information about the function. | |||
'''Dogleg method''' | '''Dogleg method''' | ||
This method can be used if <math>B_k</math> is a positive definite. The dogleg method finds an approximate solution by replacing the curved trajectory | |||
for <math>p^*\left ( \bigtriangleup \right )</math> with a path consisting of two line segments. It chooses p to minimize the model m along this path, subject to the trust-region bound. | |||
First line segments <math>p^U=-\frac{g^Tg}{g^TBg}g </math>, where <math>p^U</math>runs from the origin to the minimizer of m along the steepest descent direction. | |||
While the second line segment run from <math>p^U</math>to <math>p^B</math>, we donate this trajectory by <math>\tilde{p}\left ( \tau \right )</math> for <math>\tau \in \left [ 0,2 \right ]</math> | |||
Then a V-shaped trajectory can be determined by | |||
<math>\tilde{p}=\tau p^U </math>, when <math>0\leq \tau \leq 1 </math> | |||
<math>\tilde{p}= p^U+\left (\tau -1 \right )\left ( p^B-p^U \right ) </math>, when <math>1\leq \tau \leq 2 </math> | |||
where <math>p^B </math>=opitimal solution of quadratic model | |||
Although the dogleg strategy can be adapted to handle indefinite B, there is not much point in doing so because the full step <math>p^B</math> is not the unconstrained minimizer of m in this case. Instead, we now describe another strategy, which aims to include directions of negative | |||
curvature in the space of trust-region steps. | |||
'''Conjugated Gradient Steihaug’s Method ( CG-Steihaug)''' | |||
This is the most widely used method for the approximate solution of the trust-region problem. The method works for quadratic models <math>m_{k}</math> defined by an arbitrary symmetric <math>B_k</math> . Thus, it is not necessary for <math>B_k</math> to be positive. CG-Steihaug has the advantage of Cauchy point calculation and Dogleg method which is super-linear convergence rate and inexpensive costs. | |||
Given<math>\epsilon > 0 </math> | |||
Set <math>p_0=0,r_0=g,d_0=-r_0 </math> | |||
if<math>\left \| r_0 \right \|< \epsilon </math> | |||
return <math>p=p0</math> | |||
for <math>j=0,1,2,...</math> | |||
if <math>d_j^TB_kd_j\leq 0 </math> | |||
Find <math>\tau </math> such that minimizes <math>m\left ( p \right )</math> and satisfies<math>\left \| p \right \|=\Delta </math> | |||
return p; | |||
Set <math>\alpha _j=r_j^Tr_j/d_j^TB_kd_j</math> | |||
Set <math> p_{j+1}=p_j+\alpha _jd_j</math> | |||
if <math>\left \| p_{j+1} \right \|\geq \Delta</math> | |||
Find <math>\tau \geq 0</math> such that <math>p=p_{j}+\tau d_{j}</math> satisfies <math>\left \| p \right \|=\Delta </math> | |||
return p; | |||
Set <math>r_{j+1}=r_j+\alpha _jB_kd_j</math> | |||
if <math> \left \| r_{j+1} \right \|< \epsilon \left \| r_{0} \right \|</math> | |||
return <math>p=p_{j+1}</math> | |||
Set <math>\beta _{j+1} = r_{j+1}^{T}r_{j+1}/r_j^Tr_j</math> | |||
Set <math>d_{j+1}= r_{j+1}+ \beta _{j+1}d_j</math> | |||
end(for) | |||
'''Global Convergence''' | |||
To study the convergence of trust region, we have to study how much reduction can we achieve at each | |||
iteration (similar to line search method). Thus, we derive an estimate in the following form: | |||
<math>m_k\left ( 0 \right )-m_k\left ( p_k \right )\geq c_1\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup k,\frac{\left \| \bigtriangledown f_k\right \|}{\left \| B_k \right \|} \right )</math> for <math>c_1\in \left [ 0,1 \right ]</math> | |||
For cauchy point, <math>c_1</math>=0.5 | |||
that is | |||
<math>m_k\left ( 0 \right )-m_k\left ( p_k \right )\geq 0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup k,\frac{\left \| \bigtriangledown f_k\right \|}{\left \| B_k \right \|} \right )</math> | |||
we first consider the case of <math>\bigtriangledown f_k^TB_k\bigtriangledown f_k\leq 0</math> | |||
<math>m_k\left ( p_k^c \right )-m_k\left ( 0 \right )\geq m_k\left ( \bigtriangleup _k\bigtriangledown f_k/\left \| \bigtriangledown f_k \right \| \right )</math> | |||
<math>=-\frac{\bigtriangleup _k}{\left \| \bigtriangledown f_k \right \|}\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\ \bigtriangledown f_k^TB_k\bigtriangledown f_k</math> | |||
<math>\leq -\bigtriangleup _k\left \| \bigtriangledown f_k \right \|</math> | |||
<math>\leq -\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{B_k} \right )</math> | |||
For the next case, consider <math>\bigtriangledown f_k^TB_k\bigtriangledown f_k> 0</math> and | |||
<math>\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}\leq 1</math> | |||
we then have <math>\tau =\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}</math> | |||
so | |||
<math>m_k\left ( p_k^c \right )-m_k\left ( 0 \right )= -\frac{\left \| \bigtriangledown f_k \right \|^4}{\bigtriangledown f_k^TB_k\bigtriangledown f_k}+0.5\bigtriangledown f_k^TB_k\bigtriangledown f_k\frac{\left \| \bigtriangledown f_k \right \|^4}{\left ( \bigtriangledown f_k^TB_k\bigtriangledown f_k \right )^2}</math> | |||
<math>=-0.5\frac{\left \| \bigtriangledown f_k \right \|^4}{\bigtriangledown f_k^TB_k\bigtriangledown f_k}</math> | |||
<math>\leq -0.5\frac{\left \| \bigtriangledown f_k \right \|^4}{\left \| B_k \right \|\left \| \bigtriangledown f_k \right \|^2}</math> | |||
<math>=-0.5\frac{\left \| \bigtriangledown f_k \right \|^2}{\left \| B_k \right \|}</math> | |||
<math>\leq -0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{\left \| B_k \right \|} \right )</math>, | |||
since <math>\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}\leq 1</math> does not hold, thus | |||
<math>\bigtriangledown f_k^TB_k\bigtriangledown f_k< \frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k}</math> | |||
From the definition of <math>p_c^k</math> , we have <math>\tau =1</math>, therefore | |||
<math>m_k\left ( p_k^c \right )-m_k\left ( 0 \right )= -\frac{\bigtriangleup _k}{\left \| \bigtriangledown f_k \right \|}\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\bigtriangledown f_k^TB_k\bigtriangledown f_k</math> | |||
<math>\leq -\bigtriangleup _k\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k}</math> | |||
<math>=-0.5\bigtriangleup _k\left \| \bigtriangledown f_k \right \|</math> | |||
<math>\leq -0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{\left \| B_k \right \|} \right )</math> | |||
=Numerical example= | =Numerical example= | ||
Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's fminunc as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method. | |||
Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960<ref>H. H. Rosenbrock, An Automatic Method for Finding the Greatest or Least Value of a Function, ''The Computer Journal'', Volume 3, Issue 3, 1960, Pages 175–184, <nowiki>https://doi.org/10.1093/comjnl/3.3.175</nowiki></ref>, which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's <code>fminunc</code> as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method. | |||
The function is defined by | The function is defined by | ||
| Line 29: | Line 178: | ||
The starting point chosen is <math>x=0</math> <math>y=0 | The starting point chosen is <math>x=0</math> <math>y=0 | ||
</math>. | </math>. | ||
[[File:Trust-region method example trajectory.png|thumb|576x576px|Trust-region method trajectory of Rosenbrock function starting from (0,0). The data points represent the optimal solutions after each iteration, ending at iteration number 16 (1,1).]] | |||
'''Iteration Process''' | '''Iteration Process''' | ||
'''Iteration 1:''' The algorithm starts from the initial point of <math>x=0</math>, <math>y=0 | |||
</math>. The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution (<math>x=0.25</math>, <math>y=0 | </math>. The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution (<math>x=0.25</math>, <math>y=0 | ||
</math>) within the trust-region is denoted as a red dot. | </math>) within the trust-region is denoted as a red dot. | ||
| Line 63: | Line 214: | ||
</math>. | </math>. | ||
| Line 70: | Line 222: | ||
</math>'''.The new iteration gives a poor prediction, therefore current best solution is unchanged and the radius for the trust | </math>'''.The new iteration gives a poor prediction, therefore the current best solution is unchanged and the radius for the trust region is decreased. | ||
... | ... | ||
| Line 202: | Line 354: | ||
=Applications= | =Applications= | ||
''' | '''Approach on Newton methods on Riemannian manifold''' | ||
Absil et. Al (2007) proposed a trust-region approach for improving the Newton method on the Riemannian manifold<ref>Absil, PA., Baker, C. & Gallivan, K(2007). Trust-Region Methods on Riemannian Manifolds, ''Found Comput Math 7'', Page 303–330, <nowiki>https://doi.org/10.1007/s10208-005-0179-9</nowiki></ref>. The trust-region approach optimizes a smooth function on a Riemannian manifold in three ways. First, the exponential mapping is relaxed to general retractions with a view to reducing computational complexity. Second, a trust region approach is applied for both local and global convergence. Third, the trust-region approach allows early stopping of the inner iteration under criteria that preserve the convergence properties of the overall algorithm. | |||
'''Approach on policy optimization''' | |||
Schulman et. al (2015) proposed trust-region methods for optimizing stochastic control policies and developed a practical algorithm called Trust Region Policy Optimization (TRPO)<ref>Schulman, J., et al. (2015). Trust region policy optimization, ''International conference on machine learning'', <nowiki>http://proceedings.mlr.press/v37/schulman15</nowiki></ref>. The method is scalable and effective for optimizing large nonlinear policies such as neural networks. It can optimize nonlinear policies with tens of thousands of parameters, which is a major challenge for model-free policy search. | |||
=Conclusion= | |||
The trusted region is a powerful method that can update the objective function in each step to ensure the model is always getting improved while keeping the previously learned knowledge as the baseline. Unlike line search methods, trust region can be used in non-convex approximate models, making such class of iterative methods more reliable, robust and applicable to ill-conditioned problems<ref>Yuan, Y. X. (2000). A review of trust region algorithms for optimization, ''Iciam conference'', <nowiki>https://doi.org/10.4236/blr.2019.104046</nowiki></ref>. Recently, due to its capability to address large-scale problems<ref>Lin, C. J., Weng, R. C., & Keerthi, S. S. (2008). Trust region Newton method for large-scale logistic regression, ''Journal of Machine Learning Research'', <nowiki>https://www.jmlr.org/papers/volume9/lin08b/lin08b.pdf</nowiki></ref><ref>Rojas, M., Santos, S. A., & Sorensen, D. C. (2008). MATLAB software for large-scale trust-region subproblems and regularization, ''ACM Transactions on Mathematical Software'', <nowiki>https://doi.org/10.1145/1326548.1326553</nowiki></ref><ref>Wu, Y., Mansimov, E., Grosse, R. B., Liao, S., & Ba, J. (2017). Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation, ''Advances in neural information processing systems'', <nowiki>https://proceedings.neurips.cc/paper/2017/file/361440528766bbaaaa1901845cf4152b-Paper.pdf</nowiki></ref>, trust region has been paired with several machine-learning topics, including tuning parameter selection<ref>Geminiani, E., Marra, G., & Moustaki, I. (2021). Single-and Multiple-Group Penalized Factor Analysis: A Trust-Region Algorithm Approach with Integrated Automatic Multiple Tuning Parameter Selection, ''psychometrika'', Page 65-69, <nowiki>https://doi.org/10.1007/s11336-021-09751-8</nowiki></ref>, ridge function<ref>Gross, J. C., Seshadri, P., & Parks, G. (2020). Optimisation with intrinsic dimension reduction: A ridge informed trust-region method, ''AIAA Scitech 2020 Forum'', <nowiki>https://doi.org/10.2514/6.2020-0157</nowiki></ref>, reinforcement learning<ref>Kuba, J. G., Chen, R., Wen, M., Wen, Y., Sun, F., Wang, J., & Yang, Y. (2021). Trust region policy optimisation in multi-agent reinforcement learning, ''arXiv preprint arXiv:2109.11251'', <nowiki>https://arxiv.org/pdf/2109.11251.pdf</nowiki></ref>, etc., to develop more robust numerical algorithms. It is believed that the trust region method will have more far-reaching development in a wider range of fields in the near future. | |||
=References= | =References= | ||
<references /> | |||
Latest revision as of 01:18, 16 December 2021
Autor: Chun-Yu Chou, Ting-Guang Yeh, Yun-Chung Pan, Chen-Hua Wang (CHEME 6800, Fall 2021)
Introduction
Trust region method is a numerical optimization method that is employed to solve non-linear programming (NLP) problems[1]. Instead of finding an objective solution of the original function, the method defines a neighborhood around the current best solution as a trust region in each step (typically by using a quadratic model), which is capable of representing the function appropriately, to derive the next local optimum. Different from line search[2], the model selects the direction and step size simultaneously. For example, in a minimization problem, if the decrease in the value of the optimal solution is not sufficient since the region is too large to get close to the minimizer of the objective function, the region should be shrunk to find the next best point. On the other hand, if such a decrease is significant, it is believed that the model has an adequate representation of the problem. Generally, the step direction depends on the extent that the region is altered in the previous iteration[3].
Methodology and theory
The quadratic model function is based on derivative information at and possibly also on information accumulated from previous iterations and steps.
where
, and is symmetric matrix.
Taylor’s theorem is used as a mathematical tool to study minimizers of smooth functions.
The first two terms of are assumed to be identical to the first two terms of the Taylor-series expansion.
The difference between and is O. Therefore, when is small, the approximation error is small.
To obtain each step, we seek a solution to the subproblem as shown below.
s.t
The strategies for finding approximate solutions are introduced as follows, which achieve at least as so-called Cauchy point. This point is simply the minimizer of along the steepest descent direction that is subject to the trust region bound.
Cauchy point calculation
Similar to the line search method which does not require optimal step lengths to be convergent, the trust-region method is sufficient for global convergence purposes to find an approximate solution that lies within the trust region. Cauchy step is an inexpensive method( no matrix factorization) to solve trust-region subproblem. Furthermore, the Cauchy point has been valued because it can be globally convergent. Following is a closed-form equation of the Cauchy point.
where
Although it is inexpensive to apply the Cauchy point, the steepest descent methods sometimes perform poorly. Thus, we introduce some improving strategies. The improvement strategies is based on where it contains valid curvature information about the function.
Dogleg method
This method can be used if is a positive definite. The dogleg method finds an approximate solution by replacing the curved trajectory
for with a path consisting of two line segments. It chooses p to minimize the model m along this path, subject to the trust-region bound.
First line segments , where runs from the origin to the minimizer of m along the steepest descent direction.
While the second line segment run from to , we donate this trajectory by for
Then a V-shaped trajectory can be determined by
, when
, when
where =opitimal solution of quadratic model
Although the dogleg strategy can be adapted to handle indefinite B, there is not much point in doing so because the full step is not the unconstrained minimizer of m in this case. Instead, we now describe another strategy, which aims to include directions of negative
curvature in the space of trust-region steps.
Conjugated Gradient Steihaug’s Method ( CG-Steihaug)
This is the most widely used method for the approximate solution of the trust-region problem. The method works for quadratic models defined by an arbitrary symmetric . Thus, it is not necessary for to be positive. CG-Steihaug has the advantage of Cauchy point calculation and Dogleg method which is super-linear convergence rate and inexpensive costs.
Given
Set
if
return
for
if
Find such that minimizes and satisfies
return p;
Set
Set
if
Find such that satisfies
return p;
Set
if
return
Set
Set
end(for)
Global Convergence
To study the convergence of trust region, we have to study how much reduction can we achieve at each
iteration (similar to line search method). Thus, we derive an estimate in the following form:
for
For cauchy point, =0.5
that is
we first consider the case of
For the next case, consider and
we then have
so
,
since does not hold, thus
From the definition of , we have , therefore
Numerical example
Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960[4], which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's fminunc as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method.
The function is defined by
The starting point chosen is .
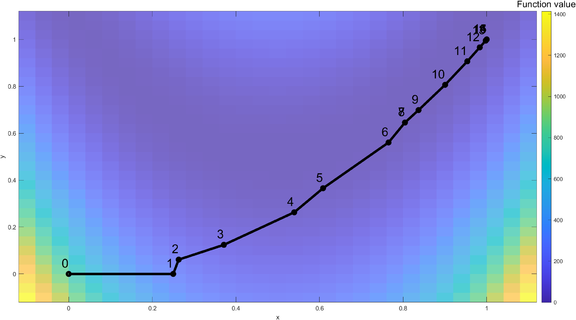
Iteration Process
Iteration 1: The algorithm starts from the initial point of , . The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution (, ) within the trust-region is denoted as a red dot.
Iteration 2: Start with , . The new iteration gives a good prediction, which increases the trust-region's size. The new optimal solution within the trust-region is , .
Iteration 3: Start with , . The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is , .
...
Iteration 7: Start with , . The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is , .
Iteration 8: Start with , .The new iteration gives a poor prediction, therefore the current best solution is unchanged and the radius for the trust region is decreased.
...
At the 16th iteration, the global optimal solution is found, , .
| Iterations | f(x) | x | y | Norm of step | First-order optimality |
|---|---|---|---|---|---|
| 1 | 1 | 0.25 | 0 | 1 | 2 |
| 2 | 0.953125 | 0.263178 | 0.061095 | 0.25 | 12.5 |
| 3 | 0.549578 | 0.371152 | 0.124076 | 0.0625 | 1.63 |
| 4 | 0.414158 | 0.539493 | 0.262714 | 0.125 | 2.74 |
| 5 | 0.292376 | 0.608558 | 0.365573 | 0.218082 | 5.67 |
| 6 | 0.155502 | 0.765122 | 0.560477 | 0.123894 | 0.954 |
| 7 | 0.117347 | 0.804353 | 0.645444 | 0.25 | 7.16 |
| 8 | 0.0385147 | 0.804353 | 0.645444 | 0.093587 | 0.308 |
| 9 | 0.0385147 | 0.836966 | 0.69876 | 0.284677 | 0.308 |
| 10 | 0.0268871 | 0.90045 | 0.806439 | 0.0625 | 0.351 |
| 11 | 0.0118213 | 0.953562 | 0.90646 | 0.125 | 1.38 |
| 12 | 0.0029522 | 0.983251 | 0.9659 | 0.113247 | 0.983 |
| 13 | 0.000358233 | 0.99749 | 0.994783 | 0.066442 | 0.313 |
| 14 | 1.04121e-05 | 0.999902 | 0.999799 | 0.032202 | 0.0759 |
| 15 | 1.2959e-08 | 1 | 1 | 0.005565 | 0.00213 |
| 16 | 2.21873e-14 | 1 | 1 | 0.000224 | 3.59E-06 |
Applications
Approach on Newton methods on Riemannian manifold
Absil et. Al (2007) proposed a trust-region approach for improving the Newton method on the Riemannian manifold[5]. The trust-region approach optimizes a smooth function on a Riemannian manifold in three ways. First, the exponential mapping is relaxed to general retractions with a view to reducing computational complexity. Second, a trust region approach is applied for both local and global convergence. Third, the trust-region approach allows early stopping of the inner iteration under criteria that preserve the convergence properties of the overall algorithm.
Approach on policy optimization
Schulman et. al (2015) proposed trust-region methods for optimizing stochastic control policies and developed a practical algorithm called Trust Region Policy Optimization (TRPO)[6]. The method is scalable and effective for optimizing large nonlinear policies such as neural networks. It can optimize nonlinear policies with tens of thousands of parameters, which is a major challenge for model-free policy search.
Conclusion
The trusted region is a powerful method that can update the objective function in each step to ensure the model is always getting improved while keeping the previously learned knowledge as the baseline. Unlike line search methods, trust region can be used in non-convex approximate models, making such class of iterative methods more reliable, robust and applicable to ill-conditioned problems[7]. Recently, due to its capability to address large-scale problems[8][9][10], trust region has been paired with several machine-learning topics, including tuning parameter selection[11], ridge function[12], reinforcement learning[13], etc., to develop more robust numerical algorithms. It is believed that the trust region method will have more far-reaching development in a wider range of fields in the near future.
References
- ↑ Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization, Cambridge university press, https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf
- ↑ Nocedal, J., & Wright, S. (2006). Numerical optimization, Springer Science & Business Media, https://www.math.uci.edu/~qnie/Publications/NumericalOptimization.pdf
- ↑ Erway, J. B., Gill, P. E., & Griffin, J. D. (2009). Iterative methods for finding a trust-region step, SIAM Journal on Optimization, https://www.math.uci.edu/~qnie/Publications/NumericalOptimization.pdf
- ↑ H. H. Rosenbrock, An Automatic Method for Finding the Greatest or Least Value of a Function, The Computer Journal, Volume 3, Issue 3, 1960, Pages 175–184, https://doi.org/10.1093/comjnl/3.3.175
- ↑ Absil, PA., Baker, C. & Gallivan, K(2007). Trust-Region Methods on Riemannian Manifolds, Found Comput Math 7, Page 303–330, https://doi.org/10.1007/s10208-005-0179-9
- ↑ Schulman, J., et al. (2015). Trust region policy optimization, International conference on machine learning, http://proceedings.mlr.press/v37/schulman15
- ↑ Yuan, Y. X. (2000). A review of trust region algorithms for optimization, Iciam conference, https://doi.org/10.4236/blr.2019.104046
- ↑ Lin, C. J., Weng, R. C., & Keerthi, S. S. (2008). Trust region Newton method for large-scale logistic regression, Journal of Machine Learning Research, https://www.jmlr.org/papers/volume9/lin08b/lin08b.pdf
- ↑ Rojas, M., Santos, S. A., & Sorensen, D. C. (2008). MATLAB software for large-scale trust-region subproblems and regularization, ACM Transactions on Mathematical Software, https://doi.org/10.1145/1326548.1326553
- ↑ Wu, Y., Mansimov, E., Grosse, R. B., Liao, S., & Ba, J. (2017). Scalable trust-region method for deep reinforcement learning using kronecker-factored approximation, Advances in neural information processing systems, https://proceedings.neurips.cc/paper/2017/file/361440528766bbaaaa1901845cf4152b-Paper.pdf
- ↑ Geminiani, E., Marra, G., & Moustaki, I. (2021). Single-and Multiple-Group Penalized Factor Analysis: A Trust-Region Algorithm Approach with Integrated Automatic Multiple Tuning Parameter Selection, psychometrika, Page 65-69, https://doi.org/10.1007/s11336-021-09751-8
- ↑ Gross, J. C., Seshadri, P., & Parks, G. (2020). Optimisation with intrinsic dimension reduction: A ridge informed trust-region method, AIAA Scitech 2020 Forum, https://doi.org/10.2514/6.2020-0157
- ↑ Kuba, J. G., Chen, R., Wen, M., Wen, Y., Sun, F., Wang, J., & Yang, Y. (2021). Trust region policy optimisation in multi-agent reinforcement learning, arXiv preprint arXiv:2109.11251, https://arxiv.org/pdf/2109.11251.pdf





















![{\displaystyle \tau \in \left[0,2\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb7df23cc0913ba505a19ff31059689caa16a938)
























![{\displaystyle c_{1}\in \left[0,1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f44f6895ef086c1521d88f2dc2b6146dbbd3d38a)


































