Trust-region methods

Autor: Chun-Yu Chou, Ting-Guang Yeh, Yun-Chung Pan, Chen-Hua Wang (CHEME 6800, Fall 2021)

Introduction

Trust region method is a numerical optimization method that is employed to solve non-linear programming (NLP) problems. Instead of finding an objective solution of the original function, the method defines a neighborhood around the current best solution as a trust region in each step (typically by using quadratic model), which is capable of representing the function appropriately, in order to derive the next local optimum. Different from line search, the model selects the direction and step size simultaneously. For example, in a minimization problem, if the decrease in the value of optimal solution is not sufficient since the region is too large to get close to the minimizer of the objective function, the region should be shrunk to find the next best point. On the other hand, if such decrease is significant, it is believed that the model has adequate representation to the problem. Generally, the step direction depends on extent that the region is altered in the previous iteration.

Methodology and theory

The quadratic model function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k} is based on derivative information at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} and possibly also on information accumulated from previous iterations and steps.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^TB_kp}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k=f(x_k), \bigtriangledown f_k=\bigtriangledown f(x_k)} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} is symmetric matrix.

Taylor’s theorem is used as a mathematical tool to study minimizers of smooth functions.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k + p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^T\bigtriangledown ^2f(x_k + tp)p}

The first two terms of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k} are assumed to be identical to the first two terms of the Taylor-series expansion.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + O(||p^2||)}

The difference between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k(p)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f (x_k + p)} is O. Therefore, when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} is small, the approximation error is small.

To obtain each step, we seek a solution to the subproblem as shown below.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min_{p\in\R} m_{k}(p)=f_{k} +\bigtriangledown f_k^Tp + 1/2p^TB_kp}

s.t Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||p^2||\leqq\Delta _k}

The strategies for finding approximate solutions are introduced as follows, which achieve at least as so-called Cauchy point. This point is simply the minimizer of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k} along the steepest descent direction that is subject to the trust region bound.

Cauchy point calculation

Similar to line serach method which do not require optimal step lengths to be convergent, trust-region method is suffficient for global convergence purpose to find an approximate solution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} that lies within trust region. Cauchy step Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k^c} is an unexpensive method( no matrix factorization) to solve trust-region subproblem. Furthermore, Cauchy point has been valued due to the fact that it can globally convergent. Following is a closed-form equations of the Cauchy point.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k^c=-\tau _k\frac{\Delta k}{\left \| \bigtriangledown f_k \right \|}\bigtriangledown f_k}

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \tau _k={\begin{cases}1,&{\text{if }}\bigtriangledown f_k^TB_k\bigtriangledown f_k\leq 0\\min\left ( \left \| \bigtriangledown f_k \right \|^{3}/\left ( \bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k \right ),1 \right ),&{\text{otherwise }}\end{cases}}}

Although it is unexpensive to apply Cauchy point, steepest descent methods sometimes performs poorly. Thus, we introduce some improving strategy. The improvement strategies is based on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} where it contains valid curvature information about the function.

Dogleg method

This method can be used if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} is a positive definite. The dogleg method finds an approximate solution by replacing the curved trajectory

for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^*\left ( \bigtriangleup \right )} with a path consisting of two line segments. It chooses p to minimize the model m along this path, subject to the trust-region bound.

First line segments Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^U=-\frac{g^Tg}{g^TBg}g } , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^U} runs from the origin to the minimizer of m along the steepest descent direction.

While the second line segment run from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^U} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^B} , we donate this trajectory by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p}\left ( \tau \right )} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \in \left [ 0,2 \right ]}

Then a V-shaped trajectory can be determined by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p}=\tau p^U } , when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq \tau \leq 1 }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{p}= p^U+\left (\tau -1 \right )\left ( p^B-p^U \right ) } , when Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1\leq \tau \leq 2 }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^B } =opitimal solution of quadratic model

Although the dogleg strategy can be adapted to handle indefinite B, there is not much point in doing so because the full step Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p^B} is not the unconstrained minimizer of m in this case. Instead, we now describe another strategy, which aims to include directions of negative

curvature in the space of trust-region steps.

Conjugated Gradient Steihaug’s Method ( CG-Steihaug)

This is the most widely used method for the approximate solution of the trust-region problem. The method works for quadratic models Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_{k}} defined by an arbitrary symmetric Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} . Thus, it is not necessary for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle B_k} to be positive. CG-Steihaug has the advantage of Cauchy point calculation and Dogleg method which is super-linear convergence rate and unexpensive costs .

GivenFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon > 0 }

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_0=0,r_0=g,d_0=-r_0 }

ifFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| r_0 \right \|< \epsilon }

return Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=p0}

for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=0,1,2,...}

if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_j^TB_kd_j\leq 0 }

Find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau } such that minimizes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\left ( p \right )} and satisfiesFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p \right \|=\Delta }

return p;

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha _j=r_j^Tr_j/d_j^TB_kd_j}

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_{j+1}=p_j+\alpha _jd_j}

if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p_{j+1} \right \|\geq \Delta}

Find Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau \geq 0} such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=p_{j}+\tau d_{j}} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| p \right \|=\Delta }

return p;

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{j+1}=r_j+\alpha _jB_kd_j}

if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left \| r_{j+1} \right \|< \epsilon \left \| r_{0} \right \|}

return Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=p_{j+1}}

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta _{j+1} = r_{j+1}^{T}r_{j+1}/r_j^Tr_j}

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{j+1}= r_{j+1}+ \beta _{j+1}d_j}

end(for)

Global Convergence

To study the convergence of trust region, we have to study how much reduction can we achieve at each

iteration (similar to line search method). Thus, we derive an estimate in the following form:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k\left ( 0 \right )-m_k\left ( p_k \right )\geq c_1\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup k,\frac{\left \| \bigtriangledown f_k\right \|}{\left \| B_k \right \|} \right )} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1\in \left [ 0,1 \right ]}

For cauchy point, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1} =0.5

that is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k\left ( 0 \right )-m_k\left ( p_k \right )\geq 0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup k,\frac{\left \| \bigtriangledown f_k\right \|}{\left \| B_k \right \|} \right )}

we first consider the case of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown f_k^TB_k\bigtriangledown f_k\leq 0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k\left ( p_k^c \right )-m_k\left ( 0 \right )\geq m_k\left ( \bigtriangleup _k\bigtriangledown f_k/\left \| \bigtriangledown f_k \right \| \right )}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-\frac{\bigtriangleup _k}{\left \| \bigtriangledown f_k \right \|}\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\ \bigtriangledown f_k^TB_k\bigtriangledown f_k}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -\bigtriangleup _k\left \| \bigtriangledown f_k \right \|}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{B_k} \right )}

For the next case, consider Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown f_k^TB_k\bigtriangledown f_k> 0} and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}\leq 1}

we then have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau =\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}}

so

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k\left ( p_k^c \right )-m_k\left ( 0 \right )= -\frac{\left \| \bigtriangledown f_k \right \|^4}{\bigtriangledown f_k^TB_k\bigtriangledown f_k}+0.5\bigtriangledown f_k^TB_k\bigtriangledown f_k\frac{\left \| \bigtriangledown f_k \right \|^4}{\left ( \bigtriangledown f_k^TB_k\bigtriangledown f_k \right )^2}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-0.5\frac{\left \| \bigtriangledown f_k \right \|^4}{\bigtriangledown f_k^TB_k\bigtriangledown f_k}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -0.5\frac{\left \| \bigtriangledown f_k \right \|^4}{\left \| B_k \right \|\left \| \bigtriangledown f_k \right \|^2}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-0.5\frac{\left \| \bigtriangledown f_k \right \|^2}{\left \| B_k \right \|}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{\left \| B_k \right \|} \right )} ,

since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k\bigtriangledown f_k^TB_k\bigtriangledown f_k}\leq 1} does not hold, thus

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigtriangledown f_k^TB_k\bigtriangledown f_k< \frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k}}

From the definition of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_c^k} , we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tau =1} , therefore

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_k\left ( p_k^c \right )-m_k\left ( 0 \right )= -\frac{\bigtriangleup _k}{\left \| \bigtriangledown f_k \right \|}\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\bigtriangledown f_k^TB_k\bigtriangledown f_k}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -\bigtriangleup _k\left \| \bigtriangledown f_k \right \|^2+0.5\frac{\bigtriangleup _k^2}{\left \| \bigtriangledown f_k \right \|^2}\frac{\left \| \bigtriangledown f_k \right \|^3}{\bigtriangleup _k}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-0.5\bigtriangleup _k\left \| \bigtriangledown f_k \right \|}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \leq -0.5\left \| \bigtriangledown f_k \right \|min\left ( \bigtriangleup _k,\frac{\left \| \bigtriangledown f_k \right \|}{\left \| B_k \right \|} \right )}

Numerical example

Here we will use the trust-region method to solve a classic optimization problem, the Rosenbrock function. The Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is often used as a performance test problem for optimization algorithms. This problem is solved using MATLAB's fminunc as the solver, with 'trust-region' as the solving algorithm which uses the preconditioned conjugate method.

The function is defined by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min f(x,y)=100(y-x^2)^2+(1-x)^2}

The starting point chosen is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } .

Trust-region method trajectory of Rosenbrock function starting from (0,0). The data points represent the optimal solutions after each iteration, ending at iteration number 16 (1,1).

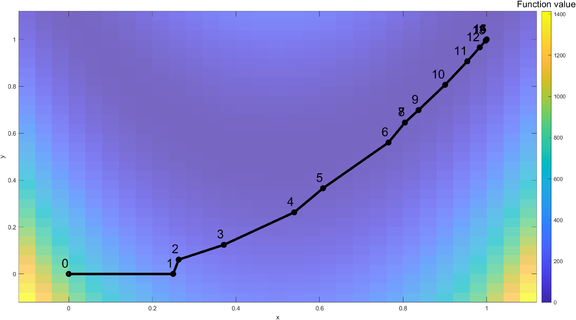
Iteration Process

Iteration 1: The algorithm starts from the initial point of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } . The Rosenbrock function is visualized with a color coded map. For the first iteration, a full step was taken and the optimal solution (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.25} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } ) within the trust-region is denoted as a red dot.

Iteration 2: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.25 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0 } . The new iteration gives a good prediction, which increases the trust-region's size. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.263177536 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.061095029 } .

Iteration 3: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.263177536 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.061095029 } . The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.371151679 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.124075855 } .

...

Iteration 7: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.765122406 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.560476539 } . The new iteration gives a poor prediction, which decreases the trust-region's size to improve the model's validity. The new optimal solution within the trust-region is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.804352654 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.645444179 } .

Iteration 8: Start with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0.804352654 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0.645444179 } .The new iteration gives a poor prediction, therefore current best solution is unchanged and the radius for the trust-region is decreased.

...

At the 16th iteration, the global optimal solution is found, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=1 } , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=1 } .

Summary of all iterations

Iterations	f(x)	x	y	Norm of step	First-order optimality
1	1	0.25	0	1	2
2	0.953125	0.263178	0.061095	0.25	12.5
3	0.549578	0.371152	0.124076	0.0625	1.63
4	0.414158	0.539493	0.262714	0.125	2.74
5	0.292376	0.608558	0.365573	0.218082	5.67
6	0.155502	0.765122	0.560477	0.123894	0.954
7	0.117347	0.804353	0.645444	0.25	7.16
8	0.0385147	0.804353	0.645444	0.093587	0.308
9	0.0385147	0.836966	0.69876	0.284677	0.308
10	0.0268871	0.90045	0.806439	0.0625	0.351
11	0.0118213	0.953562	0.90646	0.125	1.38
12	0.0029522	0.983251	0.9659	0.113247	0.983
13	0.000358233	0.99749	0.994783	0.066442	0.313
14	1.04121e-05	0.999902	0.999799	0.032202	0.0759
15	1.2959e-08	1	1	0.005565	0.00213
16	2.21873e-14	1	1	0.000224	3.59E-06

Applications

Approach on Newton methods on Riemannian manifold

Absil et. Al (2007) proposed a trust-region approach for improving the Newton method on the Riemannian manifold. The trust-region approach optimizes a smooth function on a Riemannian manifold in three ways. First, the exponential mapping is relaxed to general retractions with a view to reducing computational complexity. Second, a trust region approach is applied for both local and global convergence. Third, the trust-region approach allows early stopping of the inner iteration under criteria that preserve the convergence properties of the overall algorithm.

Approach on policy optimization

Schulman et. al (2015) proposed trust-region methods for optimizing stochastic control policies and developed a practical algorithm called Trust Region Policy Optimization (TRPO). The method is scalable and effective for optimizing large nonlinear policies such as neural networks. It can optimize nonlinear policies with tens of thousands of parameters, which is a major challenge for model-free policy search.

Conclusion

Trusted region is a powerful method that can update the objective function in each step to ensure the model is always getting improved while keeping the previously learnt knowledge as the baseline. Unlike line search methods, trust region can be used in non-convex approximate models, making such class of iterative methods more reliable, robust and applicable to ill-conditioned problems. Recently, due to its capability to address large-scale problems, trust region has been paired with several machine-learning topics, including tuning parameter selection</ref>, ridge function, reinforcement learning</ref>, ridge function, etc., to develop more robust numerical algorithms. It is believed that the trust region method will have more far-reaching development in a wider range of fields in the near future.