Unit commitment problem
Authors: Fah Kumdokrub, Malcolm Hegeman, Kapil Khanal (SYSEN 6800 Fall 2021)
Introduction
Unit commitment(UC) is a fundamentally NP-hard, mixed-integer nonlinear, non-convex optimization problem. It is used for optimizing the power generators schedule such that their operating cost is kept low over some time units(planning horizon) and within operating requirements[1]. The problem involves integer decision variables- to operate the generators and the level of production from generators. This avoids the need for constantly running the generators.
Higher generation from renewable energy sources (RES) and responsive demand participation has made the UC problem a hard challenge, mainly due to the unpredictability and the high variability of RES[2]
Theory, methodology, and/or algorithmic discussions
Mixed Integer Non-Linear Programming
The Unit Commitment Problem (UC) is a large-scale mixed-integer nonlinear program for finding the low-cost operating schedule for power generators. These problems typically have quadratic objective functions and nonlinear, non-convex transmission constraints. Typically both of these are linearized for the computational speed up[3]
Objective function =
such that
Here is the cost vector associated with , such that the objective function is to minimize system operation cost. The vectors represent the feasible generation schedule, maximum power available, and the on/off status for generator , respectively. The matrix determines how the generator interacts with the system requirements[3].
General technical constraints presented are [3]
- Convex productions costs
- Minimum and maximum output levels
- Ramping constraints
- Minimum up and downtime
Dynamic Programming Based Approach
Dynamic programming is an optimization approach that transforms a complex problem into a sequence of simpler problems; its essential characteristic is the multistage nature of the optimization procedure[4]. It takes some creativity in coming up with the formulations of dynamic programming for a problem. Also, various heuristics are applied to decrease the search space and computation time. Following is the dynamic programming problem formulation [5]
where
Flowchart for the UC problem by Dynamic programming
-
Fig. 1 Flowchart provided on [5]
Other methods in literature
Apart from these two methods, there are other several methods outlined [5]
- Priority List Method
- Lagrangian Relaxation method
- Branch and Bound Method
- Genetic algorithm based approach
Numerical example
Single Period Unit Commitment
Consider an electricity market with a particular load profile, as seen below. This demand varies throughout the course of a 6-hour period and must be satisfied by the electrical energy output from a set of three generators. Each generator has a set energy output limit, as well as unit production cost associated with energy generation. Each generator may be in an on or off state and may be started or stopped throughout the 6-hour period. The utility may wish to operate the system so that the load demand is met while minimizing cost.
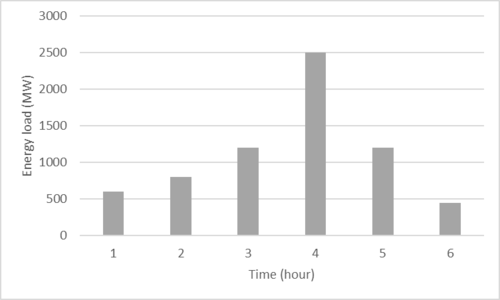
Solution
The following variables are assigned to the system:
set of generators indexed by i
Set of time intervals indexed by t
power output of generator i
cost of unit generation of generator i
binary on / off decision of generator i at time t
minimum output of generator i
maximum output of generator i
The three generators have the following characteristics:
Table 1 Generator power and unit cost
| G1 | G2 | G3 | |
| Power (MW) | 800 | 700 | 1200 |
| $ / MWh | 88 | 110 | 125 |
To determine the generator schedule, we carry out the following optimization problem to meet demand over the 6-hour period, while minimize operating cost, using a dynamic programming approach.
min
such that
`
The feasible unit combinations (states) of the generators are determined by calculating the power output for each generator combination and denoting which combination is able to satisfy the energy demand at each interval.
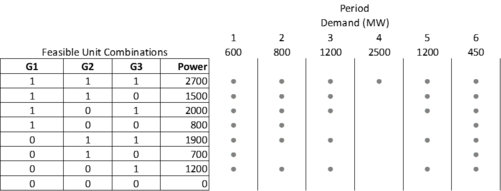
Costs are then calculated for each combination and the optimum combination that minimizes cost for each period may be selected, as seen below.
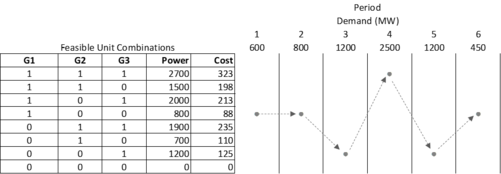
Applications
Unit commitment problems can be further adjusted for components that reflect the real-world problem. A simple categorization can be divided into two major groups. One is related to the commitment of power generation/production/manufacturing process, and the other group involves output allocation to the committed units, often known as unit commitment and economic dispatch [6].
Single-Period Unit Commitment
This type of problem usually optimizes the number of power generators for each facility/plant to meet the demand in a specific period. Although this might not be the case study in real-world scenarios, starting off with this type of unit commitment optimization problem might help check the correctness of other constraints before adding the complexity of time and other power generating units’ components.
Multi-Period Unit Commitment
Many times, the production of power should be planned in advance. This planned period could be for months, weeks, or even overnight to avoid under or over-power generation and minimize the total number of generators needed. And these problems would require a multi-period unit commitment optimization.
Unit Commitment with Additional Constraints
There are many more criteria that can be added to the unit commitment problem to truly reflect the system. Some scenarios may be required reserve constraints to ensure sufficient supply in response to a spike in demand [7]. Ramping constraints can also be added since the generators take time to start and stop the process which both affect the cost and amount of power output [7]. Types of power affect the optimization whether they come from a single source or multiple sources [7] [8].
Unit Commitment and Economic Dispatch
With any attributes to the unit commitment problem, the economic aspects are always involved meaning that the allocation of power generation (energy output) for each committing unit must be economical with all the costs and revenues. Power generator plants not only need to meet the demand, but they also need to operate in the most economical ways, at the lowest possible cost or the highest possible profit. There are many costs involved in generating power, for example, the cost per unit of power generations, the cost of shutting down or starting up the generator, the cost of over generating power since it may cause damage to the plant, and there are many other costs and benefits that could be considered to the problem.
Commercialized unit commitment software is also available for use. For example, Power Optimisation company developed a software named POWEROP which is more generalized to wide ranges of users or power companies, customized software for Northern Ireland Electricity (NIE), and software developed specifically for the British Electricity Trading and Transmission Arrangements (BETTA) [8]. Software for NIE considers power from multiple sources, including gas, coal, and oil-fired steam [7]. Additionally, software for BETTA can generate electricity prices for both the general market and individuals by contract [8]. The software was developed from a multi-stage mixed-integer linear programming (MILP) and adapted the constraints to serve customers’ specific requirements [8].
Conclusion
The unit commitment problem considers how to best deploy energy generation resources to meet energy demand imposed by the market, while optimizing for some target – typically operating costs. There are several methods that may be utilized to solve the UC problem, including Mixed Integer Non-Linear Programming and Dynamic Programming based approaches. The implications of the UC problem extend far beyond the cost saving benefits, including resource conservation and sustainability domains.
References
- ↑ Frangioni, A., & Gentile, C. (2006). Solving nonlinear single-unit commitment problems with ramping constraints. Operations Research, 54(4), 767–775. https://doi.org/10.1287/opre.1060.0309
- ↑ Abdou,I., & Tkiouat, M. (2018). Unit commitment problem in electrical power system: A literature review. International Journal of Electrical and Computer Engineering (IJECE), 8(3), 1357. https://doi.org/10.11591/ijece.v8i3.pp1357-1372
- ↑ 3.0 3.1 3.2 Knueven, B., Ostrowski, J., & Watson, J.-P. (2020). On mixed-integer programming formulations for the unit commitment problem. INFORMS Journal on Computing. https://doi.org/10.1287/ijoc.2019.0944
- ↑ Dynamic Programming. (n.d.). Retrieved November 28, 2021, from http://web.mit.edu/15.053/www/AMP-Chapter-11.pdf.
- ↑ 5.0 5.1 5.2 Krishna Mohan, R., Gopichand Naik, M., & Rajendra Prasad, S. (2021). A comparative study of unit commitment problem by dynamic programming and genetic algorithm. Lecture Notes in Electrical Engineering, 61–77. https://doi.org/10.1007/978-981-15-8439-8_6
- ↑ A.J. Conejo, L. Baringo, “Power System Operations,” Power Electronics and Power Systems, p. 197-232, 2018, doi:https://link.springer.com/chapter/10.1007%2F978-3-319-69407-8_7
- ↑ 7.0 7.1 7.2 7.3 L.A. Wolsey, Integer Programming. Wiley, 1998.
- ↑ 8.0 8.1 8.2 8.3 “Unit Commitment and Economic Dispatch Software to Optimise the Short-Term Scheduling of Electrical Power Generation” https://msi-jp.com/xpress/learning/square/unit_en.pdf (accessed Nov. 13, 2021).













![Fig. 1 Flowchart provided on [5]](/images/thumb/8/88/DP.png/499px-DP.png)










