Line search methods

Authors: Lihe Cao, Zhengyi Sui, Jiaqi Zhang, Yuqing Yan, and Yuhui Gu (6800 Fall 2021).

Introduction

Line search method is an iterative approach to find a local minimum of a multidimensional nonlinear function using the function's gradients. It aims at finding an acceptable step length witch satisfies certain standard conditions. Line search and trust-region methods are two fundamental strategies for locating the new iterate given the current point. With the ability to solve the unconstrained optimization problem, line search is widely used in many cases including machine learning, game theory and other fields.

Generic Line Search Method

Basic Algorithm

• Pick the starting point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0}
• Repeat the following steps until Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_k:=f(x_k)} coverges to a local minimum :
  • Choose a descent direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} starting at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} , defined as: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f_{k}^\top p_{k}<0} for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f_k \not =0}
  • Find a step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k>0} so that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k+\alpha_kp_k)<f_k}
  • Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1}=x_k+\alpha_k p_k}

Search Direction for Line Search

The direction of the line search should be chosen to make Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} decrease moving from point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1}} , and it is usually related to the gradient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f_k} . The most obvious direction is the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \nabla f_k} because it is the one to make Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} decreases most rapidly. This claim can be verified by Taylor's theorem:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k+\alpha)=f(x_k)+\alpha p^\top\nabla f_k+\frac{1}{2}\alpha^2p^\top f(x_k+tp)p} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t\in (0, \alpha) } .

The rate of change in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} along the direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} is the coefficient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} . Therefore, the unit direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p} of most rapid decrease is the solution to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min\ p^\top\nabla f_k}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{s.t.}\ \ ||p||=1} .

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=\frac{-\nabla f_k}{||\nabla f_k||}} is the solution and this direction is orthogonal to the contours of the function. In the following sections, this will be used as the default direction of the line search.

However, the steepest descent direction is not the most efficient, as the steepest descent method does not pass the Rosenbrock test (see Figure 1). Carefully designed descent directions deviating from the steepest direction can be used in practice to produce faster convergence.

Step Length

The step length is a non-negative value such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k+\alpha_k p_k)<f(x_k)} . When choosing the step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} , there is a trade off between giving a substantial reduction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} and not spending too much time finding the solution. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} is too large, then the step will overshoot, while if the step length is too small, it is time consuming to find the convergent point. An exact line search and inexact line search are needed to find the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} and more detail about these approaches will be introduced in the next section.

Convergence

For a line search algorithm to be reliable, it should be globally convergent, that is the gradient norms, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||\nabla f(x_{k})||} , should converge to zero with each iteration, i.e., Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k\to\infty} ||\nabla f(x_{k})|| = 0} .

It can be shown from Zoutendijk's theorem that if the line search algorithm satisfies (weak) Wolfe's conditions (similar results also hold for strong Wolfe and Goldstein conditions) and has a search direction that makes an angle with the steepest descent direction that is bounded away from 90°, the algorithm is globally convergent.

Zoutendijk's theorem states that, given an iteration where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} is the descent direction and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} is the step length that satisfies (weak) Wolfe conditions, if the objective Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is bounded below on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{n}} and is continuously differentiable in an open set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} containing the level set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{L}:=\{x\ |\ f(x)\leq f(x_0)\}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} is the starting point of the iteration, and the gradient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f} is Lipschitz continuous on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{N}} , then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{k=0}^{\infty}\cos^{2}\theta_{k}||\nabla f_{k}||^2 < \infty} ,

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_{k}} is the angle between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} and the steepest descent direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\nabla f(x_{k})} .

The Zoutendijk condition above implies that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k\to\infty}\cos^{2}\theta_{k}||\nabla f_{k}||^2=0} ,

by the n-th term divergence test. Hence, if the algorithm chooses a search direction that is bounded away from 90° relative to the gradient, i.e., given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon>0} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos\theta_{k}\geq\epsilon>0,\ \forall k} ,

it follows that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k\to\infty}||\nabla f_{k}||=0} .

However, the Zoutendijk condition doesn't guarantee convergence to a local minimum but only stationary points. Hence, additional conditions on the search direction is necessary, such as finding a direction of negative curvature whenever possible, to avoid converging to a nonminimizing stationary point.

Exact Search

Steepest Descent Method

Given the intuition that the negative gradient Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \nabla f_k} can be an effective search direction, steepest descent follows the idea and establishes a systematic method for minimizing the objective function. Setting Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle - \nabla f_k} as the direction, steepest descent computes the step-length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} by minimizing a single-variable objective function. More specifically, the steps of Steepest Descent Method are as follows:

Steepest Descent Algorithm

Set a starting point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0}

Set a convergence criterium Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon>0}

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = 0}

Set the maximum iteration Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle N}

While Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k \le N} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x_k) = \left.\frac{\partial f(x)}{\partial x}\right\vert_{x=x_k}}

If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x_k)\le \epsilon} :

Break

End if

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k=\underset{\alpha}{\arg\min} f(x_k-\alpha \nabla f(x_k))}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k+1}=x_k-\alpha_k \nabla f(x_k)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = k + 1}

End while

Return Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_{k}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_{k})}

Figure 1. Steepest descent does not produce convergence on the Rosenbrock function.

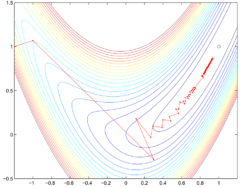
One advantage of the steepest descent method is the convergency. For a steepest descent method, it converges to a local minimum from any starting point.

Theorem: Global Convergence of Steepest Descent

Let the gradient of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f \in C^1} be uniformly Lipschitz continuous on Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^{n}} . Then, for the iterates with steepest-descent search directions, one of the following situations occurs:

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x_k) = 0} for some finite Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k}

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k \to \infty} f(x_k) = -\infty}

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{k \to \infty} \nabla f(x_k) = 0}

However, steepest descent has disadvantages in that the convergence is always slow and numerically may be not convergent (see Figure 1.)

Steepest descent method is a special case of gradient descent in that the step-length is analytically defined. However, step-lengths cannot always be computed analytically; in this case, inexact methods can be used to optimize Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} at each iteration.

Inexact Search

While minimizing an objective function using numeric methods, in each iteration, the updated objective is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\alpha) = f(x_k+\alpha p_k)} , which is a function of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} after fixing the search direction. The goal is to minimize this objective with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} . However, if one wants to solve for the exact minimum in each iteration, it could be computationally expensive and the algorithm will be time-consuming. Therefore, in practice, it is easier solve the subproblem

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \underset{\alpha}{min} \quad \phi(\alpha) = f(x_k + \alpha p_k)}

numerically and find a reasonable step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} instead, which will decrease the objective function. That is, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} satisfies Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k + \alpha p_k) \leq f(x_k)} . However, convergence to the function's minimum cannot be guaranteed, so Wolfe or Goldstein conditions need to be applied when searching for an acceptable step length.

Wolfe Conditions

This condition is proposed by Phillip Wolfe in 1969. It provide an efficient way of choosing a step length that decreases the objective function sufficiently. It consists of two conditions: Armijo (sufficient decrease) condition and the curvature condition.

Figure 2. Armijo Condition.

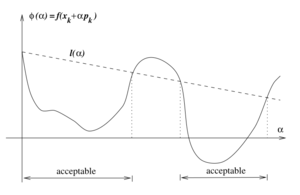
Armijo (Sufficient Decrease) Condition

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k + \alpha p_k) \leq f(x_k) + c_1 \alpha_{k} p^\top_k \nabla{f(x_k)}} ,

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1\in(0,1)} and is often chosen to be of a small order of magnitude around Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 10^{-3}} . This condition ensures the computed step length can sufficiently decrease the objective function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k)} . Only using this condition, however, it cannot be guaranteed that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_k} will converge in a reasonable number of iterations, since Armijo condition is always satisfied with step length being small enough. Therefore, the second condition below needs to be paired with the sufficient decrease condition to keep Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} from being too short.

Figure 3. Curvature Condition.

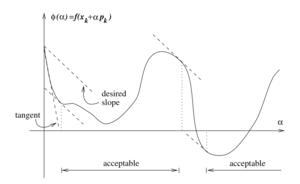
Curvature Condition

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla{f(x_k + \alpha p_k)}^\top p_k \geq c_2 \nabla{f(x_k)}^\top p_k} ,

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_2\in(c_1,1)} is much greater than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1} and is typically on the order of 0.1. This condition ensures a sufficient increase of the gradient.

This left hand side of the curvature condition is simply the derivative of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\alpha)} , thus ensuring Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} to be in the vicinity of a stationary point of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\alpha)} .

Figure 4. Goldstein Condition.

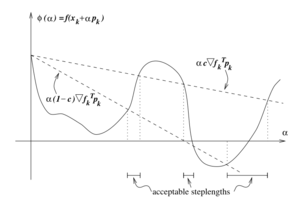
Strong Wolfe Curvature Condition

The (weak) Wolfe conditions can result in an Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} value that is not close to the minimizer of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\alpha)} . The (weak) Wolfe conditions can be modified by using the following condition called Strong Wolfe condition, which writes the curvature condition in absolute values

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |p_k \nabla{f(x_k + \alpha p_k)| \leq c_2 |p^\top_k f(x_k)}|} .

The strong Wolfe curvature condition restricts the slope of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(\alpha)} from getting too positive, hence excluding points far away from the stationary point of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} .

Goldstein Conditions

Another condition to find an appropriate step length is called Goldstein conditions:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_k) + (1-c) \alpha_k \nabla{f^\top_k} p_k \leq f(x_k + \alpha p_k) \leq f(x_k) + c \alpha_k \nabla{f^\top_k} p_k}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 \leq c \leq 1/2} . The Goldstein condition is quite similar with the Wolfe condition in that, its second inequality ensures that the step length Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} will decrease the objective function sufficiently and its first inequality keep Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha} from being too short. In comparison with Wolfe condition, one disadvantage of Goldstein condition is that the first inequality of the condition might exclude all minimizers of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} function. However, usually it is not a fatal problem as long as the objective decreases in the direction of convergence. As a short conclusion, the Goldstein and Wolfe conditions have quite similar convergence theories. Compared to the Wolfe conditions, the Goldstein conditions are often used in Newton-type methods but are not well suited for quasi-Newton methods that maintain a positive definite Hessian approximation.

Backtracking Line Search

The backtracking method is often used to find the appropriate step length and terminate line search based. The backtracking method starts with a relatively large initial step length (e.g., 1 for Newton method), then iteratively shrinking it by a contraction factor until the Armijo (sufficient decrease) condition is satisfied. The advantage of this approach is that the curvature condition needs not be considered, and the step length found at each line search iterate is ensured to be short enough to satisfy sufficient decrease but large enough to still allow the algorithm to make reasonable progress towards convergence.

The backtracking algorithm involves control parameters Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho\in(0,1)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c\in(0,1)} , and it is roughly as follows:

Choose Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0>0, \rho\in(0,1), c\in(0,1)}

Set Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\leftarrow\alpha_0}

While Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_{k}+\alpha p_{k}) > f(x_{k})+c\alpha\nabla f_{k}^{\top}p_{k}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha\leftarrow\rho\alpha}

End while

Return Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k=\alpha}

Numeric Example

As an example, we can use line search method to solve the following unconstrained optimization problem:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \min_{x_1,x_2}\ f(x)=x_1-x_2+2x_1x_2+2x_1^2+x_2^2 } .

First iteration:

We have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x)=\begin{bmatrix} 1+2x_2+4x_1\\ -1+2x_1+2x_2 \end{bmatrix}} .

Starting from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0=\begin{bmatrix} 0\\0 \end{bmatrix}} gives Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\nabla f(x_0)=\begin{bmatrix}-1\\1\end{bmatrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_0-\alpha_0\nabla f(x_0))= f(-\alpha,\alpha)=\alpha^2-2\alpha}

Taking partial derivative with respect to the above equation and set it to zero to find the minimizer Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_0=1 } Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=\begin{bmatrix}0\\0\end{bmatrix} +\alpha_0 \begin{bmatrix}-1\\1\end{bmatrix} =\begin{bmatrix}-\alpha\\ \alpha\end{bmatrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=[-1,1]}

Second iteration:

Given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_1=[-1,1]} , we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1=-\nabla f(x_1)=[1,1]} Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=[-1,1]+\alpha_1[1,1]=[-1+\alpha_1,1+\alpha_1] }

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_2)=5\alpha_1^2-2\alpha_1-1} Taking partial derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1} and set it to zero

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f(x_2)}{\partial \alpha_1}=0} Then we can get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1=0.2}

Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=[-0.8,1.2]}

Third iteration:

Given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2=-0.8,1.2]} , we have have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2=-\nabla f(x_2)=[-0.2,0.2]}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3=[-0.8,1.2]+\alpha_2[-0.2,0.2]=[0.8-0.2\alpha_2,1.2+0.2\alpha_2]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_3)=0.04\alpha_2^2-1.2-0.08\alpha_2}

Taking partial derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f(x_3)}{\partial \alpha_2}=0.08\alpha_2-0.08=0} Then we can get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_2=1}

Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3=[-1,1.4]}

Fourth iteration:

Given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_3=[-1,1.4]} , we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_3=-\nabla f(x_3)=[0.2,0.2]}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_4=[-1,1.4]+\alpha_2[0.2,0.2]=[0.2\alpha_3-1,0.2\alpha_3+1.4]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_4)=-0.08\alpha_3+0.2\alpha_3^2-1.24}

Taking partial derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_3} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f(x_4)}{\partial \alpha_3}=0.4\alpha_3-0.08=0 } Then we can get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_3=0.2}

Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_4=[-0.96,1.44]}

Fifth iteration:

Given Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_4=[-0.96,1.44]} , we have Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_4=-\nabla f(x_3)=[-0.04,0.04]}

Then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_5=[-0.96,1.4]+\alpha_3[-0.04,0.04]=[-0.96-0.04\alpha_4,0.04\alpha_4+1.44]}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x_5)= 0.0016 \alpha _4^2-0.0032 \alpha 4-1.248}

Taking partial derivative with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_4} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f(x_5)}{\partial \alpha_4}=0.00324\alpha_4-0.0032=0} Then we can get Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_4=1}

Therefore, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_5=[-1,1.48]} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla f(x_5)=[-0.04,-0.04]}

Check to see if the convergence satisfied evaluated Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||\nabla f(x_5)||} :

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle || \nabla f(x_5)||=\sqrt{(-0.04)^2+(-0.04)^2}=0.0565 } .

Since 0.0565 is relatively small and is close enough to zero, the line search is converged. The derived optimal solution is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_5=[-1,1.48]} and the optimal value is -1.25.

Applications

A common application of line search method is in minimizing the loss function in training machine learning models. For example, when training a classification model with logistic regression, gradient descent algorithm (GD), which is a classic method of line search, can be used to minimize the logistic loss and compute the coefficients by iteration till the loss function reaches converges to a local minimum. An alternative of gradient descent in machine learning domain is stochastic gradient descent (SGD). The difference is on computation expense that instead of using all training set to compute the descent, SGD simply sample one data point to compute the descent. The application of SGD reduces the computation costs greatly in large dataset compared to gradient descent.

Line search can also be applied in adaptive filtering that choose the convergence parameter so that the updated filter vector minimizes the sum of squared errors on a linear manifold.

Conclusion

Line Search is a useful strategy to solve unconstrained optimization problems. The success of the line search algorithm depends on careful consideration of the choice of both the direction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_k} and the step size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_k} .This page has introduced the basic algorithm firstly, and then includes the exact search and inexact search. The exact search contains the steepest descent, and the inexact search covers the Wolfe and Goldstein conditions, backtracking, and Zoutendijk's theorem. More approaches to solve unconstrained optimization problems can be found in trust-region methods, conjugate gradient methods, Newton's method and Quasi-Newton method.